Page 368 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 368

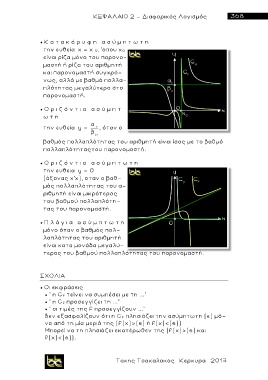
 Κ α τ α κ ό ρ υ φ η α σ ύ μ π τ ω τ η
την ευθεία x = x 0, 'οπου x 0
είναι ρίζα μόνο του παρονο-
μαστή ή ρίζα του αριθμητή
και παρονομαστή συγχρό-
νως, αλλά με βαθμό πολλα-
πλότητας μεγαλύτερο στο

παρονομαστή.

 Ο ρ ι ζ ό ν τ ι α α σ ύ μ π τ
ω τ η
α
την ευθεία y = ν , όταν ο
β
μ
βαθμός πολλαπλότητας του αριθμητή είναι ίσος με το βαθμό
πολλαπλότηταςτου παρονομαστή.

 Ο ρ ι ζ ό ν τ ι α α σ ύ μ π τ ω τ η
την ευθεια y = 0
(άξονας x’x), οταν ο βαθ-
μός πολλαπλότητας του α-

ριθμητή είναι μικρότερος
του βαθμού πολλαπλότη-
τας του παρονομαστή.

 Π λ ά γ ι α α σ ύ μ π τ ω τ η
μόνο όταν ο βαθμός πολ-
λαπλότητας του αριθμητή
είναι κατα μονάδα μεγαλύ-
τερος του βαθμού πολλαπλότητας του παρονομαστή.

ΣΧΟΛΙΑ

 Οι εκφράσεις
 " η C f τ ε ίνει να συμπέσει με τη ..."
 " η C f προσεγγίζ ε ι τη ..."
 " οι τιμές της f προσεγγίζoυ ν ..."
δεν εξασφαλίζουν ό τ ι η C f πλησιάζει την ασύμπτωτη (ε) μό-
νο από τη μία μεριά της (f(x)>(e) ή f(x)<(e))
Μπορεί να τη πλησιάζ ε ι εκατέρωθεν της (f(x)>(e) και
f(x)<(e)).

Τακης Τσακαλακος Κερκυρα 2017