Page 52 - olokliroma

52
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

β
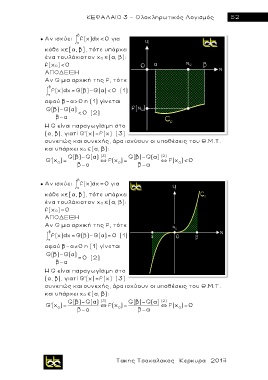
● Αν ισχύει f(x)dx 0 για
α
κάθε χ [α, β], τότε υπάρχει

ένα τουλάχιστον χ 0 (α, β):
f(x 0)<0
ΑΠΟΔΕΙΞΗ
Aν G μια αρχική της f, τότε

β
f(x)dx G(β)-G(α)< 0 (1)
α
αφού β-α>0 η (1) γίνεται
G(β)-G(α)
<0 (2)

Η G είναι παραγωγίσιμη στο
(α, β), γιατί G'(x)=f(x) (3)
συνεπώς και συνεχής, άρα ισχύουν οι υποθέσεις του Θ.Μ.Τ.

και υπάρχει χ 0 (α, β):
G(β)-G(α) (3) G(β)-G(α) (2)
G'(x ) ` f(x ) ` f(x ) 0
0 0 0

β
● Αν ισχύει f(x)dx 0 για
α
κάθε χ [α, β], τότε υπάρχει

ένα τουλάχιστον χ 0 (α, β):
f(x 0)=0
ΑΠΟΔΕΙΞΗ
Aν G μια αρχική της f, τότε

β
f(x)dx G(β)-G(α)= 0 (1)
α
αφού β-α 0 η (1) γίνεται
G(β)-G(α)
=0 (2)

Η G είναι παραγωγίσιμη στο
(α, β), γιατί G'(x)=f(x) (3)
συνεπώς και συνεχής, άρα ισχύουν οι υποθέσεις του Θ.Μ.Τ.

και υπάρχει χ 0 (α, β):
G(β)-G(α) (3) G(β)-G(α) (2)
G'(x ) ` f(x ) ` f(x ) 0
0 0 0

Τακης Τσακαλακος Κερκυρα 2017