Page 48 - olokliroma

48
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

Θ Ε Ω Ρ Ι Α ...

ΘΕΩΡΗΜΑ
Αν f είναι μια συνεχής συνάρτηση σε ένα διάστημα Δ και α
είναι ένα σημείο του Δ, τότε η συνάρτηση
x f(t)dt, χ Δ,
F(x)= α
είναι μια παράγουσα της f στο Δ. Δηλαδή ισχύει:
x f(t)dt ' = f(x), για κάθε χ Δ.
a

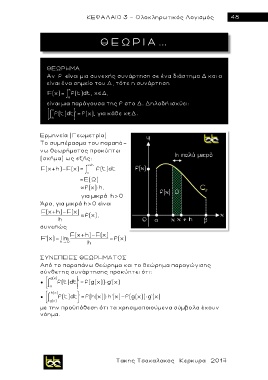
Ερμηνεία (Γεωμετρία)

Tο συμπέρασμα του παραπά-

νω θεωρήματος προκύπτει
(σχήμα) ως εξής:

x+h
F(x+h)-F(x)= x f(t)dt

=Ε(Ω)

f(x)× h,

για μικρά h>0
Άρα, για μικρά h>0 είναι

F(x+h)-F(x)
f(x),
h

συνεπώς

F'(x) = lim F(x+h)-F(x) =f(x)
h 0 h

ΣΥΝΕΠΕΙΕΣ ΘΕΩΡΗΜΑΤΟΣ
Από το παραπάνω θεώρημα και το θεώρημα παραγώγισης

σύνθετης συνάρτησης προκύπτει ότι:
g(x)
● f(t)dt ' =f(g(x))× g'(x)
α

h(x)
● f(t)dt ' =f(h(x))× h'(x)-f(g(x))× g'(x)
g(x)
με την προϋπόθεση ότι τα χρησιμοποιούμενα σύμβολα έχουν

νόημα.

Τακης Τσακαλακος Κερκυρα 2017