Page 25 - Matematika Integral

TATAP MUKA :
B. INTEGRAL SEBAGAI LUAS DAERAH DI BIDANG DATAR

Menentukan Luas daerah dengan Proses Limit
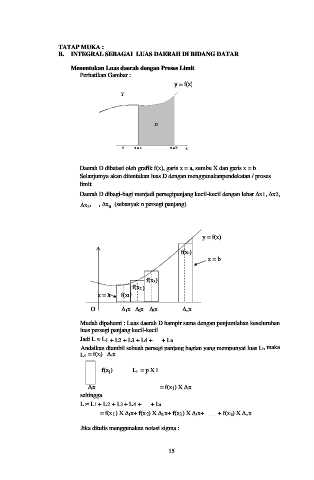
Perhatikan Gambar :
y = f(x)
y

D

0 x = a x = b x

Daerah D dibatasi oleh grafik f(x), garis x = a, sumbu X dan garis x = b.
Selanjutnya akan ditentukan luas D dengan menggunakanpendekatan / proses
limit.
Daerah D dibagi-bagi menjadi persegipanjang kecil-kecil dengan lebar x1, x2,

x 3, ... , xn. (sebanyak n persegi panjang).

y = f(x)

f(xn)
x = b

f(x3)
f(x2)
x = a f(x1)

O 1x 2x 3x nx

Mudah dipahami : Luas daerah D hampir sama dengan penjumlahan keseluruhan
luas persegi panjang kecil-kecil.
Jadi L  L1 + L2 + L3 + L4 +..... + Ln
Andaikan diambil sebuah persegi panjang bagian yang mempunyai luas Li, maka
Li = f(xi) . ix

f(xi) Li = p X l

ix = f(xi) X ix
sehingga

L ≈ L1 + L2 + L3 + L4 +..... + Ln
= f(x1) X 1x+ f(x2) X 2x+ f(x3) X 3x+ ........+ f(xn) X nx

Jika ditulis menggunakan notasi sigma :

15