Page 124 - основы милогии 1999

ч ten M1M1 "енишшенш ". LW2 тл 2 К2
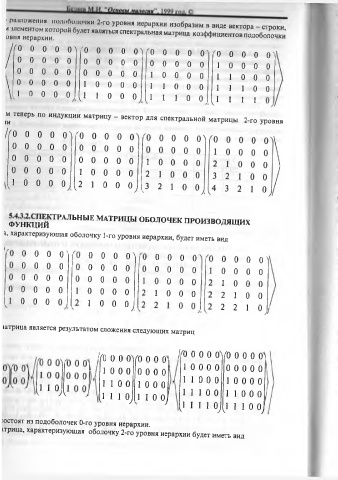
разложения подоболочки 2-го уровня иерархии изобразим
в виде вектора - строки,
л элемен том которой будет являться спектральная матрица коэффициентов подоболочки 0
овня иерархии.
о
/р О о о о о о о о о о о о о О' о
О о о
О') г0
о о о О'! г0 о о о О' "о
о
О о о о о о о о о 1 о о о о О 1 1 о 1 о о о 1
о о О
о о
о
\1;. о о о I1 1 о 1 о о о о 1 1 1 1 о 1 о О 1 1 1 о о А спектральная матрица ее подоболочек будет соответственно
о
о
о
о
о
о
I1
о
О
1
1
1
/го 0 0 0 О' Ч) О О о оЛ \
м теперь по индукции матрицу - вектор для о о о о~ о о _ о
■и спектральной матрицы 2-го уровня /1 0 0 0 0 о о о о о И
ГО 0s 10 0 0 0 0 0 0
/(О
о о о О') "о о о о о н 2 1 0 0 0 1 0 0 0 0
2 10 0 10 0 0 \3
О о о о о о о о о о 1? 2 1 0 J t21 о о; 2 1 0 0 2 1 0 0 0 //
\|4 3 2 1 О 0 /
О о о о о о о о о о 1 о 3 2 1 °J
о о о о о 1 о о о о 2 1
1 о о о о I2 1 о о о к3 которая состоит из подоболочек 1-го уровня иерархии.
7 2 Тогда для спектральной матрицы оболочки 3-го уровня иерархии будем иметь
соответственно
'0 0 0 0 О'
функциТТРАЛЬНЫЕ МАТРИЦЫ оболочек производящих 1 0 0 0 0
4 1 0 0 0
i, характеризующая оболочку 1-го уровня иерархии, будет иметь вид
9 4 1 0 0
о о о О' о о о О') о о о о о о о О'] [16 9 4 1
о о о О о о о о о о о о о о о о Z
о о о о о о о о о о о о А спектральная матрица, характеризующая ее тонкий спектр разложения на подоболочки, будет
о о о о о о о о 1 о о о 1 о о о иметь сследующий вид
о о о 1 о о о 2 1 о о
°J/
7 2 2 1
■атрица является результатом сложения следующих матриц
!... /АО 1 0 0 0 0 0 0 0 0 0 5.4.4. ДРУГИЕ КЛАССЫ ИЕРАРХИЧЕСКИХ СТРУКТУР
О О О О' 'О О О О О']
о о о 0 0 0 0
1 1
ООО. 1
0 0 0 0
110 1 о о 10 0 0 Рассмотренный выше класс производящих функций основан на свойствах бинома
\ А 1 ioj 1 1 о 0] 1 1 1 о о 1 10 0 0 Ньютона (1-х)п. Фундаментальная особенность этой формулы заключается в том, что она
I1 1 1 10J и 1 1 о 0; отражает закономерность двойственности. Из других классов иерархических структур
рассмотрим производящие функции для структур, порождаемые числами Фиббоначи. Бытует
очень широко распространенное мнение, что весь окружающий нас мир подчинен и построен
юстоят из подоболочек 0-го уровня иерархии.
с использованием пропорций, определяемый “золотым сечением”, определяемым пропорцией
(трица, характеризующая оболочку 2-го уровня иерархии будет иметь вид
1:1,618. Анализ рядов Фиббоначи, их сходимость к “золотому сечению”, позволяет
сделать