Page 124 - 20 Euclides

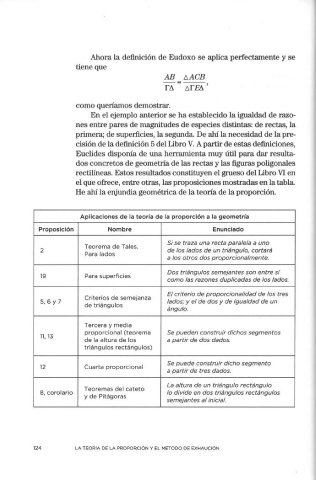
Ahora la definición de Eudoxo se aplica perfectamente y se
tiene que
AB t::,ACB
r~ = t::,I'E~'

como queríamos demostrar.
En el ejemplo anterior se ha establecido la igualdad de razo-
nes entre pares de magnitudes de especies distintas: de rectas, la
primera; de superficies, la segunda. De ahí la necesidad de la pre-
cisión de la definición 5 del Libro V. A partir de estas definiciones,
Euclides disponía de una herramienta muy útil para dar resulta-
dos concretos de geometría de las rectas y las figuras poligonales
rectilíneas. Estos resultados constituyen el grueso del Libro VI en
el que ofrece, entre otras, las proposiciones mostradas en la tabla.
He ahí la enjundia geométrica de la teoría de la proporción.

Aplicaciones de la teoría de la proporción a la geometría
Proposición Nombre Enunciado

Si se traza una recta paralela a uno
Teorema de Tales.
2 de los lados de un triángulo, cortárá
Para lados
a los otros dos proporcionalmente.
Dos triángulos semejantes son entre sí
19 Para superficies
como las razones duplicadas de los lados.
El criterio de proporcionalidad de los tres
Criterios de semejanza
5, 6 y 7 lados; y el de dos y de igualdad de un
de triángulos
ángulo.
Tercera y media
proporcional (teorema Se pueden construir dichos segmentos
11, 13
de la altura de los a partir de dos dados.
triángulos rectángulos)
Se puede construir dicho segmento
12 Cuarta proporcional
a partir de tres dados.
La altura de un triángulo rectángulo
Teoremas del cateto
8, corolario lo divide en dos triángulos rectángulos
y de Pitágoras
semejantes al inicial.

124 LA TEORIA DE LA PROPORCIÓN Y EL MÉTODO DE EXHAUCIÓN