Page 92 - 22 Euler

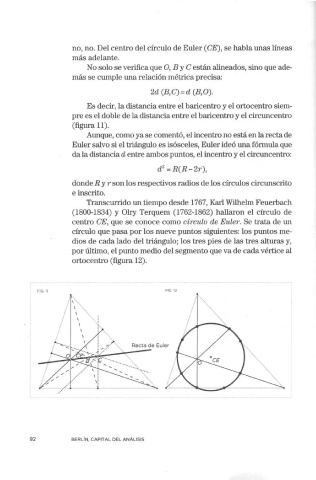
no, no. Del centro del círculo de Euler (CE), se habla unas líneas
más adelante.
No solo se verifica que O, By C están alineados, sino que ade-
más se cumple una relación métrica precisa:
2d (B, C) = d (B, O).

Es decir, la distancia entre el baricentro y el 01tocentro siem-
pre es el doble de la distancia entre el baricentro y el circuncentro
( figura 11).
Aunque, como ya se comentó, el incentro no está en la recta de
Euler salvo si el triángulo es isósceles, Euler ideó una fórmula que
da la distanciad entre ambos puntos, el incentro y el circuncentro:
2
d =R(R-2r),
donde R y r son los respectivos radios de los círculos circunscrito
e inscrito.
Transcurrido un tiempo desde 1767, Karl Wilhelm Feuerbach
(1800-1834) y Olry Terquem (1762-1862) hallaron el círculo de
centro CE, que se conoce como círculo de Euler. Se trata de un
círculo que pasa por los nueve puntos siguientes: los puntos me-
dios de cada lado del triángulo; los tres pies de las tres alturas y,
por último, el punto medio del segmento que va de cada vértice al
ortocentro (figura 12).

FIG.11 FIG. 12
' 1
/ 1 1

1
1
Recta de Euler

92 BERLÍN, CAPITAL DEL ANÁLISIS