Page 119 - 07 Schrödinger

EN PARADERO DESCONOCIDO
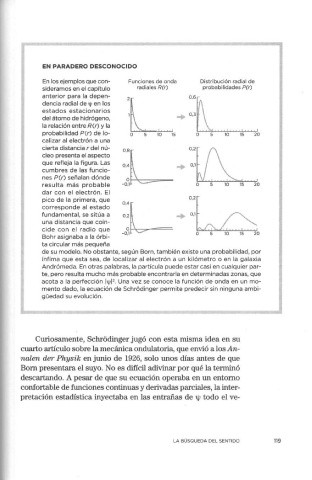
En los ejemplos que con- Funciones de onda Distribución radial de
sideramos en el capítulo radiales R(r) probabilidades P(r)
anterior para la depen-
dencia radial de ljJ en los
estados estacionarios :L .. º'~
del átomo de hidrógeno,
la relación entre R(r) y la
probabilidad P(r) de lo- O 5 10 15 10 15 20
calizar al electrón a una
cierta distanciar del nú- 0,2
cleo presenta el aspecto º·ªL
que refleja la figura. Las
cumbres de las funcio- º·: ,+ 0,1
nes P(r) señalan dónde
-0,1 L..>!-'--'-w....-'--'-w....= 1L5'--'--'-..J20
resulta más probab le
dar con el electrón. El
pico de la primera, que 0,2
corresponde al estado
fundamental, se sitúa a 0,4~
º·:
una d istancia que coin- ,+ 0,1
cide con el radio que
-0.1 o~'-'--L5'-""'"--'-10L.W.-'--'-1-'--5 '--'--'--'-'20
Bohr asignaba a la órbi-
ta circular más pequeña
de su modelo. No obstante, según Born, también existe una probabilidad, por
ínfima que esta sea, de localizar al electrón a un kilómetro o en la galaxia
Andrómeda. En otras palabras, la partícula puede estar casi en cualquier par-
te, pero resulta mucho más probable encontrarla en determinadas zonas, que
acota a la perfección lt¡,1 • Una vez se conoce la función de onda en un mo-
2
mento dado, la ecuación de Schródinger permite predecir sin ninguna ambi-
güedad su evolución.

Curiosamente, Schrodinger jugó con esta misma idea en su
cuarto artículo sobre la mecánica ondulatoria, que envió a los An-
nalen der Physik en junio de 1926, solo unos días antes de que
Bom presentara el suyo. No es difícil adivinar por qué la terminó
descartando. A pesar de que su ecuación operaba en un entorno
confortable de funciones continuas y derivadas parciales, la inter-
pretación estadística inyectaba en las entrañas de 'l(J todo el ve-

LA BÚSQUEDA DEL SENTIDO 119