Page 78 - 07 Schrödinger

FIG. 3
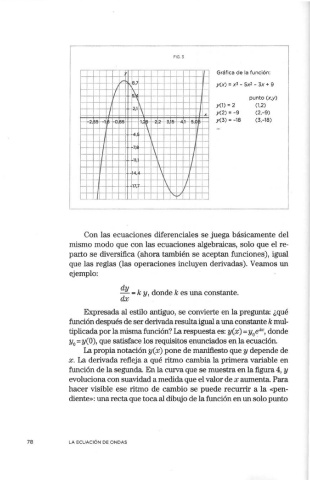
:, ·· r- Gráfica de la función:
1--+-+-+-1--+--i,<-.... -Rrl!lb,ii --+-+-1-1--+---+-1--1--+---~ y (x) = x3 - sx2 - 3x + 9
1-------/ - ~~--------- -
1--------+-, --- punto (x.y)
y (l) = 2 (1,2)
y(2) = -9 (2,-9)
y(3) = -18 (3,-18)
- ..-i!,SS-1-1Jt+ 0:Gs - -1. t-ili2+-315 - 4;1-- s,1 >/ -
f
--- - !-- · ~S-.:~t;_·;•:.=-.:-:-=-+-1---+-·--_ 1:=
-
•
---
-rr--+-+--lsr·'t
1
1
l--+-l-+++-+-l--l•-tl,!>-j--f-\'H-+-+1--1--+-+-/I 1--+-•
/
.
1-+-+-+Hl-+--+---+I 1--J---,¡......+·\\+·¡•--+-+-+-1~·-+·-++-+-l
-!--+-~¡+--- n , ----- / -
·
=F- ··-+-+-+-·l+--,;.·-·•---\ Y--l
l-+-t--t-,._,.-t--t+ -\íl4 ,a-~-- - ~·\ !-t-+-t--f- -l--
!
i J
-+--11-+-I -- '-
l '-V T J_
Con las ecuaciones diferenciales se juega básicamente del
mismo modo que con las ecuaciones algebraicas, solo que el re-
parto se diversifica (ahora también se aceptan funciones), igual
que las reglas (las operaciones incluyen derivadas). Veamos un
ejemplo:

dy = k y, donde k es una constante.
dx
Expresada al estilo antiguo, se convierte en la pregunta: ¿qué
función después de ser derivada resulta igual a una constante k mul-
tiplicada por la misma función? La respuesta es: y(x) = y ekx, donde
0
y = y(O), que satisface los requisitos enunciados en la ecuación.
0
La propia notación y(x) pone de manifiesto que y depende de
x. La derivada refleja a qué ritmo cambia la primera variable en
función de la segunda. En la curva que se muestra en la figura 4, y
evoluciona con suavidad a medida que el valor de x aumenta. Para
hacer visible ese ritmo de cambio se puede recurrir a la «pen-
diente»: una recta que toca al dibujo de la función en un solo punto

78 LA ECUACIÓN DE ONDAS