Page 80 - 07 Schrödinger

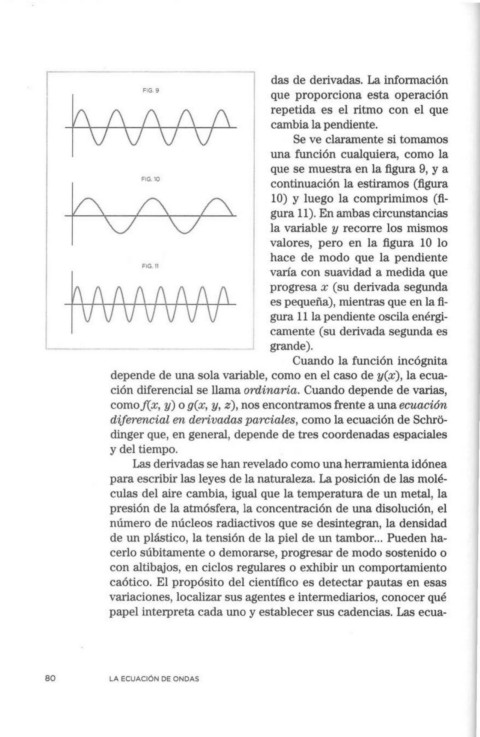
fA /\ /\ /\ das de derivadas. La información
FIG. 9
que proporciona esta operación
repetida es el ritmo con el que
VV V V cambia la pendiente.
Se ve claramente si tornarnos
una función cualquiera, corno la
que se muestra en la figura 9, y a
continuación la estirarnos (figura
10) y luego la comprimirnos (fi-
gura 11). En ambas circunstancias
V V la variable y recorre los mismos
~ figura 1 O lo
valores, pero en la
hace de modo que la pendiente
FIG. 11
varía con suavidad a medida que
progresa x (su derivada segunda
r/\!\!\/\/\!\ es pequeña), mientras que en la fi-
VvV V vVl/ gura 11 la pendiente oscila enérgi-
camente (su derivada segunda es
_________ J grande).
Cuando la función incógnita
depende de una sola variable, corno en el caso de y(x), la ecua-
ción diferencial se llama ordinaria. Cuando depende de varias,
comof(x, y) o g(x, y, z), nos encontrarnos frente a una ecuación
diferencial en derivadas parciales, como la ecuación de Schro-
dinger que, en general, depende de tres coordenadas espaciales
y del tiempo.
Las derivadas se han revelado corno una herramienta idónea
para escribir las leyes de la naturaleza. La posición de las molé-
culas del aire cambia, igual que la temperatura de un metal, la
presión de la atrnósf era, la concentración de una disolución, el
número de núcleos radiactivos que se desintegran, la densidad
de un plástico, la tensión de la piel de un tambor ... Pueden ha-
cerlo súbitamente o demorarse, progresar de modo sostenido o
con altibajos, en ciclos regulares o exhibir un comportamiento
caótico. El propósito del científico es detectar pautas en esas
variaciones, localizar sus agentes e intermediarios, conocer qué
papel interpreta cada uno y establecer sus cadencias. Las ecua-

80 LA ECUACIÓN DE ONDAS