Page 81 - 07 Schrödinger
P. 81
LA LENGUA DE LAS DERIVADAS
El sentido de las derivadas ayuda a traducir el lenguaje algo críptico de las
ecuaciones diferenciales. Veámoslo con el ejemplo ya familiar:
dy - ky.
dx
Con su solución: y(x) = y ekx
0
Tomemos el caso más sencillo:
dy
k=l = --y.
dx
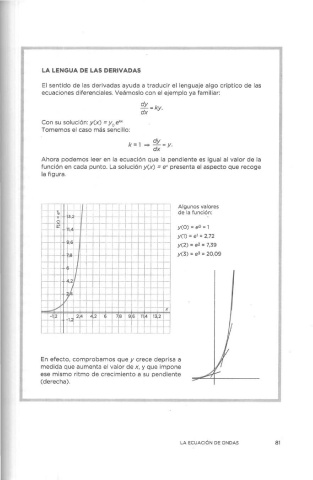
Ahora podemos leer en la ecuación que la pendiente es igual al valor de la
función en cada punto. La solución y(x) = e" presenta el aspecto que recoge
la figura.
Algunos valores
de la función:
y(O) =eº = 1
y(l) = e 1 = 2,72
y(2) = e2 = 7,39
y(3) = e3 = 20,09
En efecto, comprobamos que y crece deprisa a
medida que aumenta el valor de x, y que impone
ese mismo ritmo de crecimiento a su pendiente
(derecha).
LA ECUACIÓN DE ONDAS 81