Page 79 - 07 Schrödinger

recta pendiente con la horizontal y(x)I~- -=
(es tangente a ella) para cadax. Al
observar el ángulo que forma la

se adquiere una idea intuitiva del 1
-
-
-
-
-;,---~i--=c-----=-~-.....:..:.::::~-_ __-_::--'-'-X 1
valor de la derivada. Una pendiente
plana equivale a una derivada nula
(y no cambia con x), mientras que
una pendiente que se acerca a la
vertical corresponde a una deri-
vada que tiende al infinito (y crece
muchísimo frente a una pequeña
variación de x). En nuestro caso,
p
p
todas las pendientes son pequeñas, ~ P, --'- :--:.._~ Referencia
horizontal
es decir, se desvían poco de la ho-
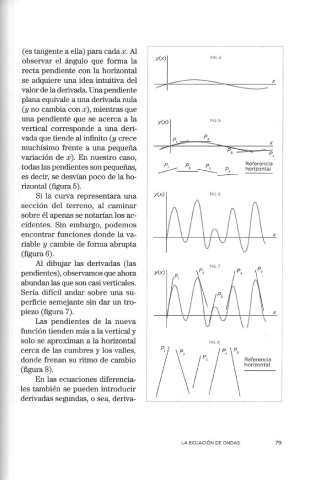
rizontal (figura 5).
Si la curva representara una y(x) FIG.6
sección del terreno, al caminar
sobre él apenas se notarian los ac-
cidentes. Sin embargo, podemos
encontrar funciones donde la va- X
riable y cambie de forma abrupta
(figura 6).
Al dibujar las derivadas (las
pendientes), observarnos que ahora y(x)
abundan las que son casi verticales.
Sería difícil andar sobre una su-
perficie semejante sin dar un tro-
piezo (figura 7). X
Las pendientes de la nueva
función tienden más a la vertical y
solo se aproximan a la horizontal FIG. 8
cerca de las cumbres y los valles,
donde frenan su ritmo de cambio Referencia
horizontal
(figura 8).
En las ecuaciones diferencia- l
les también se pueden introducir
derivadas segundas, o sea, deriva- _J

LA ECUACIÓN DE ONDA$ 79