Page 90 - 04 Max Planck

puede crecer sin línúte, por lo cual su nú-
mero es infinito (véase la figura). Si a
-----L ----+
cada onda le asignamos una cantidad fija
de energía, al ser el número de ondas po-
sible infinito, la cantidad de energía con-
tenida en la cavidad será también infinita.
La teoría de Rayleigh-Jeans era la ley
que cabía esperar a partir de los princi-
A= 2L/3 pios de la física clásica, pero nunca tuvo
~
un verdadero valor predictivo. Solo en el
A= L/2 línúte de bajas frecuencias, o longitudes
de onda larga, se aproximaba al valor ex-
perimental. Durante la primera década
A= L/4
del siglo xx los físicos más importantes
/VVVVV\ del momento, lo que incluye a Lorentz,
A= L/n Einstein, Jeans, Wien, Planck, Ehrenfest
o Poincaré, se devanaron los sesos inten~
tando comprender por qué. Hacia el final
de la década todos aceptaban que la hipó-
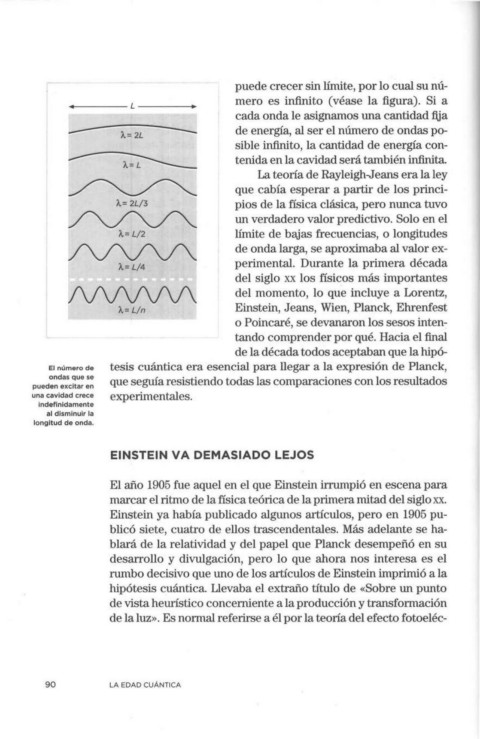
El número de tesis cuántica era esencial para llegar a la expresión de Planck,
ondas que se
pueden excitar en que seguía resistiendo todas las comparaciones con los resultados
una cavidad crece experimentales.
indefinidamente
al disminuir la
longitud de onda.

EINSTEIN VA DEMASIADO LEJOS

El año 1905 fue aquel en el que Einstein irrumpió en escena para
marcar el ritmo de la física teórica de la primera mitad del siglo xx.
Einstein ya había publicado algunos artículos, pero en 1905 pu-
blicó siete, cuatro de ellos trascendentales. Más adelante se ha-
blará de la relatividad y del papel que Planck desempeñó en su
desarrollo y divulgación, pero lo que ahora nos interesa es el
rumbo decisivo que uno de los artículos de Einstein imprimió a la
hipótesis cuántica. Llevaba el extraño título de «Sobre un punto
de vista heurístico concerniente a la producción y transformación
de la luz». Es normal referirse a él por la teoría del efecto fotoeléc-

90 LA EDAD CUÁNTICA