Page 121 - EMY SOHILAIT DASAR KALKULUS

Penyelesaian :

'
2
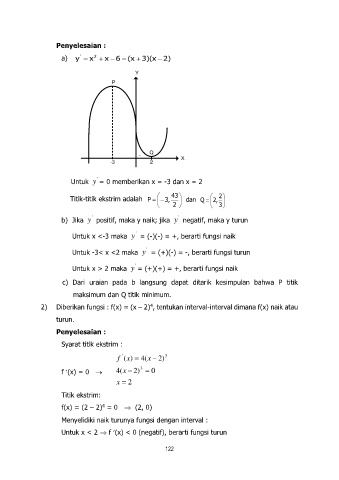
a) y  x  x  6  (x  3)(x  2)

Y
P

Q X
-3 2

'
Untuk y = 0 memberikan x = -3 dan x = 2

Titik-titik ekstrim adalah P  3, 43   dan Q   2, 2  

 2   3 
'
'
b) Jika y positif, maka y naik; jika y negatif, maka y turun
'
Untuk x <-3 maka y = (-)(-) = +, berarti fungsi naik

'
Untuk -3< x <2 maka y = (+)(-) = -, berarti fungsi turun

'
Untuk x > 2 maka y = (+)(+) = +, berarti fungsi naik
c) Dari uraian pada b langsung dapat ditarik kesimpulan bahwa P titik

maksimum dan Q titik minimum.
4
2) Diberikan fungsi : f(x) = (x – 2) , tentukan interval-interval dimana f(x) naik atau
turun.

Penyelesaian :
Syarat titik ekstrim :

f ' (x )  ( 4 x  ) 2 3

f (x) = 0  ( 4 x  ) 2 3  0
x  2

Titik ekstrim:
f(x) = (2 – 2) = 0  (2, 0)
4
Menyelidiki naik turunya fungsi dengan interval :

Untuk x < 2  f (x) < 0 (negatif), berarti fungsi turun

122