Page 124 - EMY SOHILAIT DASAR KALKULUS

kerugian dapat dianalisis dengan mengetahui penerimaan total (R) yang diperoleh dan

biaya total (C) yg dikeluarkan.
Keuntungan (profit positif, >0), didapat bila R > C, kurva R terletak diatas kurva C).

Kerugian (profit negatif,  < 0), apabila R < C, kurva R terletak dibawah kurva C).

Pulang Pokok (break-even) merupakan suatu konsep yang digunakan untuk

menganalisis jumlah minimum produk yang harus dihasilkan atau terjual agar
perusahaan tidak mengalami kerugian. Keadaan Pulang Pokok (Profit nol,  = 0),

terjadi apabila R = C dimana perusahaan tidak memperoleh keuntungan tetapi tidak

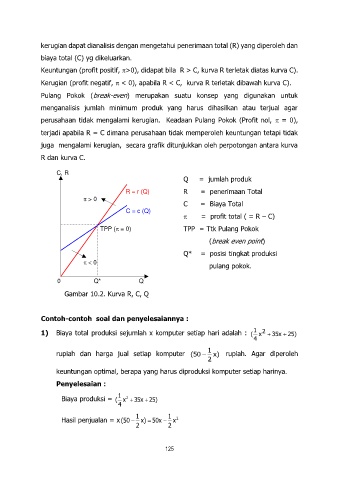
juga mengalami kerugian, secara grafik ditunjukkan oleh perpotongan antara kurva

R dan kurva C.
C, R

Q = jumlah produk

R = r (Q) R = penerimaan Total
> 0
C = Biaya Total
C = c (Q)
 = profit total ( = R – C)

TPP (= 0) TPP = Ttk Pulang Pokok

(break even point)
Q* = posisi tingkat produksi
 0
pulang pokok.

Q* Q
0
Gambar 10.2. Kurva R, C, Q

Contoh-contoh soal dan penyelesaiannya :

1 2
1) Biaya total produksi sejumlah x komputer setiap hari adalah : ( x  35x  25)
4
1
rupiah dan harga jual setiap komputer (50  x) rupiah. Agar diperoleh
2
keuntungan optimal, berapa yang harus diproduksi komputer setiap harinya.

Penyelesaian :

Biaya produksi = ( 1 x  35x  25)
2
4
1 1
Hasil penjualan = x(50  x)  50x  x
2
2 2

125