Page 62 - 10A4

2 Cho tam giác ABC có A(x A ; y A ), B(x B ; y B ) và C(x C ; y C ). Tåa đë trång tâm
G(x G ; y G ) cõa tam giác ABC đưñc tính theo công thùc


x A + x B + x C
x G =

3
y A + y B + y C

 y G = .
3
E CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI

{ DẠNG 1. Tìm tọa độ của điểm và độ dài đại số của một véc-tơ trên
− →
trục (O; e )
Phương pháp gi£i. Căn cù vào đành nghĩa tåa đë cõa điºm và đë dài đ¤i sè
cõa véc-tơ.
−−→ − →
Điºm M có tåa đë a ⇔ OM = a e , vîi O là điºm gèc.
−−→ −−→ − →
Véc-tơ AB có đë dài đ¤i sè là m = AB ⇔ AB = m e .
N¸u M và N có tåa đë l¦n lưñt là a và b thì MN = b − a.

{ DẠNG 2. Xác định tọa độ của véc-tơ và của điểm trên mặt phẳng tọa
độ Oxy
Phương pháp gi£i. Căn cù vào đành nghĩa tåa đë cõa mët véc-tơ và tåa đë cõa
mët điºm trên m°t ph¯ng tåa đë Oxy.
− →
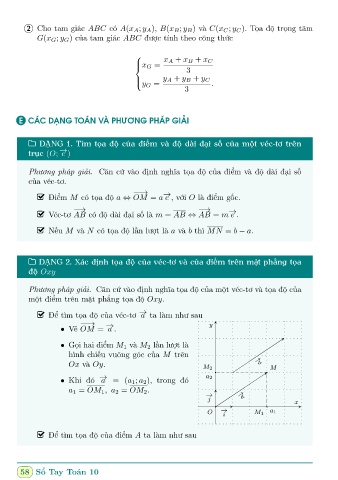
Đº tìm tåa đë cõa véc-tơ a ta làm như sau
−−→ − → y
• V³ OM = a .
• Gåi hai điºm M 1 và M 2 l¦n lưñt là
hình chi¸u vuông góc cõa M trên → −
Ox và Oy. a
M 2 M
− → a 2
• Khi đó a = (a 1 ; a 2 ), trong đó
a 1 = OM 1 , a 2 = OM 2 .
−→ → −
j a
x
O −→ a 1
i M 1
Đº tìm tåa đë cõa điºm A ta làm như sau

58 Sê Tay Toán 10