Page 13 - Geometria
P. 13
Geometría 5° San Marcos
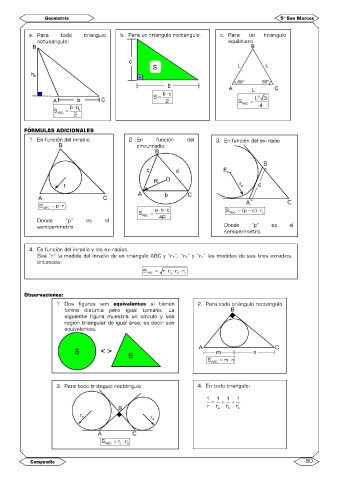
a. Para todo triángulo b. Para un triángulo rectángulo. c. Para un triángulo
obtusángulo: equilátero
b c
S = L 2 3
2 S ABC =
b h 4
S ABC = 2 b
FÓRMULAS ADICIONALES
1. En función del inradio 2. En función del 3. En función del ex-radio
circunradio
S ABC = p r a b c
S ABC = 4R S ABC = (p − c ) r c
Donde “p” es el
semiperímetro. Donde “p” es el
semiperímetro.
4. En función del inradio y los ex-radios.
Sea “r” la medida del inradio de un triángulo ABC y “ra”, “rb” y “rc” las medidas de sus tres exradios.
entonces:
S = r r r r
ABC
a
b
c
Observaciones:
1. Dos figuras son equivalentes si tienen 2. Para todo triángulo rectángulo
forma distinta pero igual tamaño. La
siguiente figura muestra un círculo y una
región triangular de igual área, es decir son
equivalentes.
S ABC = m n
3. Para todo triángulo rectángulo. 4. En todo triángulo:
1 1 1 1
= + +
r r a r b r c
S ABC = r r
c
a
Compendio -80-