Page 160 - KM Matematika_BS_KLS_IX
P. 160
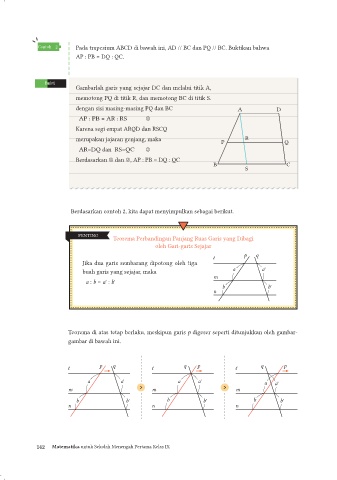
Contoh 2 Pada trapesium ABCD di bawah ini, AD // BC dan PQ // BC. Buktikan bahwa
AP : PB = DQ : QC.
Bukti
Gambarlah garis yang sejajar DC dan melalui titik A,
memotong PQ di titik R, dan memotong BC di titik S.
dengan sisi masing-masing PQ dan BC A D
AP : PB = AR : RS ①
Karena segi empat ARQD dan RSCQ
merupakan jajaran genjang, maka P R Q
AR=DQ dan RS=QC ②
Berdasarkan ① dan ②, AP : PB = DQ : QC
B C
S
Berdasarkan contoh 2, kita dapat menyimpulkan sebagai berikut.
PENTING Teorema Perbandingan Panjang Ruas Garis yang Dibagi
oleh Gari-garis Sejajar
l p q
Jika dua garis sembarang dipotong oleh tiga
buah garis yang sejajar, maka a a'
m
a : b = a' : b'
b b'
n
Teorema di atas tetap berlaku, meskipun garis p digeser seperti ditunjukkan oleh gambar-
gambar di bawah ini.
l p q l q p l q p
a a' a a' a a'
m m m
b b' b b' b b'
n n n
142 Matematika untuk Sekolah Menengah Pertama Kelas IX