Page 122 - Thesis PhD Anger by Chaichana
P. 122
๑๐๔
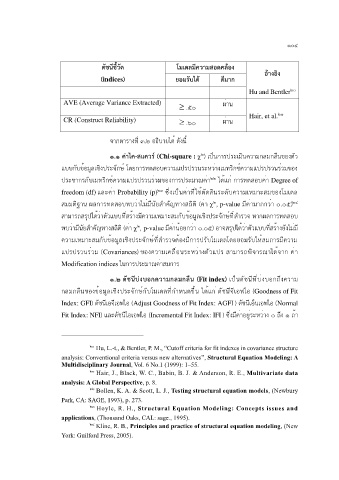
ดัชนีชี้วัด โมเดลมีควำมสอดคล้อง
(indices) ยอมรับได้ ดีมำก อ้ำงอิง
๒๐
Hu and Bentler
AVE (Average Variance Extracted) ผ่าน
.๕๐
๒๑
CR (Construct Reliability) .๖๐ ผ่าน Hair, et al.
จากตารางที่ ๓.๒ อธิบายได้ ดังนี้
๑.๑ ค่ำไค-สแควร์ (Chi-square : ) เป็นการประเมินความกลมกลืนของตัว
๒
แบบกับข้อมูลเชิงประจักษ์ โดยการทดสอบความแปรปรวนระหว่างเมทริกซ์ความแปรปรวนร่วมของ
๒๒
ประชากรกับเมทริกซ์ความแปรปรวนร่วมของการประมาณค่า ได้แก่ การทดสอบค่า Degree of
๒๓
freedom (df) และค่า Probability (p) ซึ่งเป็นค่าที่ใช้ตัดสินระดับความเหมาะสมของโมเดล
๒๔
๒
สมมติฐาน ผลการทดสอบพบว่าไม่มีนัยสำคัญทางสถิติ (ค่า , p-value มีค่ามากกว่า ๐.๐๕)
สามารถสรุปได้ว่าตัวแบบที่สร้างมีความเหมาะสมกับข้อมูลเชิงประจักษ์ที่สำรวจ หากผลการทดสอบ
พบว่ามีนัยสำคัญทางสถิติ (ค่า , p-value มีค่าน้อยกว่า ๐.๐๕) อาจสรุปได้ว่าตัวแบบที่สร้างยังไม่มี
๒
ความเหมาะสมกับข้อมูลเชิงประจักษ์ที่สำรวจต้องมีการปรับโมเดลโดยยอมรับให้สมการมีความ
แปรปรวนร่วม (Covariances) ของความเคลื่อนระหว่างตัวแปร สามารถพิจารณาได้จาก ค่า
Modification indices ในการประมาณค่าสมการ
๑.๒ ดัชนีบ่งบอกควำมกลมกลืน (Fit index) เป็นดัชนีที่บ่งบอกถึงความ
กลมกลืนของข้อมูลเชิงประจักษ์กับโมเดลที่กำหนดขึ้น ได้แก่ ดัชนีจีเอฟไอ (Goodness of Fit
Index: GFI) ดัชนีเอจีเอฟไอ (Adjust Goodness of Fit Index: AGFI ) ดัชนีเอ็นเอฟไอ (Normal
Fit Index: NFI) และดัชนีไอเอฟไอ (Incremental Fit Index: IFI ) ซึ่งมีค่าอยู่ระหว่าง ๐ ถึง ๑ ถ้า
๒๐ Hu, L.-t., & Bentler, P. M., “Cutoff criteria for fit indexes in covariance structure
analysis: Conventional criteria versus new alternatives”, Structural Equation Modeling: A
Multidisciplinary Journal, Vol. 6 No.1 (1999): 1–55.
๒๑ Hair, J., Black, W. C., Babin, B. J. & Anderson, R. E., Multivariate data
analysis: A Global Perspective, p. 8.
๒๒ Bollen, K. A. & Scott, L. J., Testing structural equation models, (Newbury
Park, CA: SAGE, 1993), p. 273.
๒๓ Hoyle, R. H., Structural Equation Modeling: Concepts issues and
applications, (Thousand Oaks, CAL: sage., 1995).
๒๔ Kline, R. B., Principles and practice of structural equation modeling, (New
York: Guilford Press, 2005).