Page 30 - MODUL DARING SISTEM PENGATURAN_Neat
P. 30
2.4 TEOREMA-TEOREMA DALAM TRANSFORMASI
LAPLACE
2.4.1 Teorema Translasi/Pergeseran pada Sumbu-t
Sebuah f(t) yang didefinisikan untuk t > 0, ketika digeser ke kanan sejauh α
satuan, maka persamaannya menjadi :
= 0 untuk t
.................................................................. (2-36)
)
= f ( t − untuk t
f(t)
f(t) f(t - )
A A
t t
0 0
(a) (b)
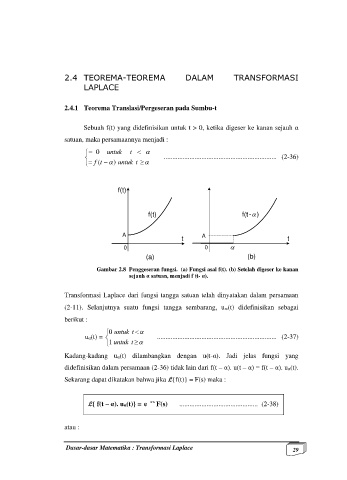
Gambar 2.8 Penggeseran fungsi. (a) Fungsi asal f(t). (b) Setelah digeser ke kanan
sejauh α satuan, menjadi f (t- α).
Transformasi Laplace dari fungsi tangga satuan telah dinyatakan dalam persamaan
(2-11). Selanjutnya suatu fungsi tangga sembarang, u(t) didefinisikan sebagai
berikut :
untuk t
0
uα(t) = ...................................................................... (2-37)
1 untuk t
Kadang-kadang uα(t) dilambangkan dengan u(t-α). Jadi jelas fungsi yang
didefinisikan dalam persamaan (2-36) tidak lain dari f(t – α). u(t – α) = f(t – α). uα(t).
Sekarang dapat dikatakan bahwa jika L{f(t)} = F(s) maka :
L{ f(t – α). uα(t)} = e − s F(s) .............................................. (2-38)
atau :
Dasar-dasar Matematika : Transformasi Laplace 29