Page 137 - Untitled
P. 137
מתמטיקה ,תשע"ג ,מועד ב ,מס' + 317 ,035807נספח
الرياض ّيات ،2013 ،الموعد "ب" ،رقم + 317 ،035807ملحق
= ) k ، f(xهو بارامتر لا يساوي . 0 kx معطاة الدالّة . 5
,nx
أ .جد مجال تعريف الدالّة ). f(x
ب ( 1) .جد بالنسبة لأ ّية ق َيم kتوجد للدالّة ) f(xنهاية عظمى.
معطى أ ّنه في المجال x21تحصل الدالّة ) f(xعلى جميع الق َيم y#- 2وعلى هذه
الق َيم فقط.
) (2جد قيمة . k
) ( 3معطى أي ًضا أ ّن المستقيم x =1هو خ ّط التقارب الوحيد للدالّة ). f(x
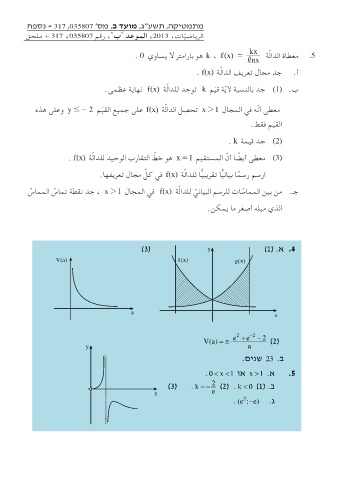
ارسم رس ًما بيان ًّيا تقريب ًّيا للدالّة ) f(xفي ك ّل مجال تعريفها.
جـ .من بين المما ّسات للرسم البيان ّي للدالّة ) f(xفي المجال ، x21جد نقطة تما ّس المما ّس
الذي ميله أصغر ما يمكن.
.4א(3) y (1) .
)V(a) f (x) g(x
ax
)V(a = ⋅π e2 + e−2 − 2 )(2
a
y
ב 23 .שנים.
א x >1 .או . 0 < x <1 .5
)(3 =.k − 2 )(2 .k<0 ב(1) .
e
x
ג. (e2;−e) .