Page 12 - 柯博智

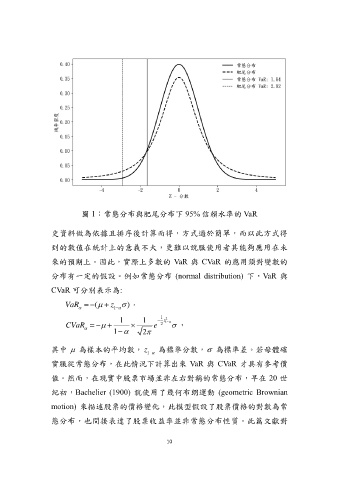
圖 1：常態分布與肥尾分布下 95% 信賴水準的 VaR

史資料做為依據且排序後計算而得，方式過於簡單，而以此方式得

到的數值在統計上的意義不大，更難以說服使用者其能夠應用在未

來的預期上。因此，實際上多數的 VaR 與 CVaR 的應用須對變數的

分布有一定的假設。例如常態分布 (normal distribution) 下，VaR 與

CVaR 可分別表示為:

VaR  (   z   1   )，

1 1  1 z 1 
2
CVaR     e 2  ，



1  2

其中  為樣本的平均數， z 1  為標準分數， 為標準差。若母體確

實服從常態分布，在此情況下計算出來 VaR 與 CVaR 才具有參考價

值。然而，在現實中股票市場並非左右對稱的常態分布，早在 20 世

紀初，Bachelier (1900) 就使用了幾何布朗運動 (geometric Brownian

motion) 來描述股票的價格變化，此模型假設了股票價格的對數為常

態分布，也間接表達了股票收益率並非常態分布性質。此篇文獻對

10