Page 82 - BUKU MATEMATIKA DASAR 1_Neat

−ℎ ℎ
f’_(0)= lim f’+(0)= lim
−
ℎ→0 − ℎ ℎ→0 ℎ
f’_(0)= -1 f’+(0)= 1

dari hasil di atas tampak f’_(0) dan f’+(0), keduanya ada tapi tidak sama, jadi f’(0)
tidak ada.

3.2.2 HUBUNGAN KETERDIFERENSIALAN DENGAN KEKONTINUAN

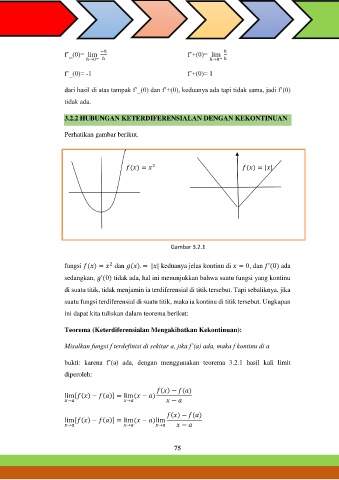
Perhatikan gambar berikut.

2
( ) = ( ) = | |

Gambar 3.2.1

2
fungsi ( ) = dan ( ). = | | keduanya jelas kontinu di = 0, dan ’(0) ada
sedangkan, ’(0) tidak ada, hal ini menunjukkan bahwa suatu fungsi yang kontinu

di suatu titik, tidak menjamin ia terdiferensial di titik tersebut. Tapi sebaliknya, jika
suatu fungsi terdiferensial di suatu titik, maka ia kontinu di titik tersebut. Ungkapan

ini dapat kita tuliskan dalam teorema berikut:

Teorema (Keterdiferensialan Mengakibatkan Kekontinuan):

Misalkan fungsi f terdefinisi di sekitar a, jika f’(a) ada, maka f kontinu di a

bukti: karena f’(a) ada, dengan menggunakan teorema 3.2.1 hasil kali limit
diperoleh:

( ) − ( )
lim[ ( ) − ( )] = lim( − )
→ → −

( ) − ( )
lim[ ( ) − ( )] = lim( − )lim
→ → → −

75
