Page 85 - BUKU MATEMATIKA DASAR 1_Neat

2
2
2
( + ℎ) − ( ) 2 +4 ℎ + 2ℎ + 1 − 2 − 1
′
( ) = lim = lim
ℎ→0 + ℎ ℎ→0 + ℎ
( + ℎ) − ( )
′
( ) = lim = lim 4 + 2ℎ
ℎ→0 + ℎ ℎ→0 +
( + ℎ) − ( )
′ ( ) = lim = 4
ℎ→0 + ℎ

Jelas f’(x) = 4x terdefinisi setiap x Ɛ (-1,2)

3.2.4 NOTASI LAIN UNTUK TURUNAN

Pada bagian awal pasal ini telah dikemukan fungsi turunan pertama dari = ( )
terhadap fungsi variable bebas x ditulis ’( ). turunan pertama ini dapat diruliskan

pula dengan notasi lainnya sebagai berikut:

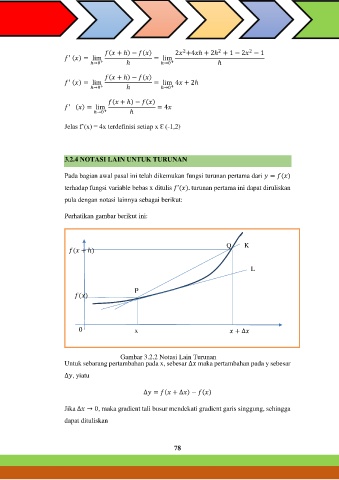
Perhatikan gambar berikut ini:

( + ℎ) Q K
P

L

P
( )

0 x + ∆

Gambar 3.2.2 Notasi Lain Turunan
Untuk sebarang pertambahan pada x, sebesar ∆ maka pertambahan pada y sebesar

∆ , yiatu

∆ = ( + ∆ ) − ( )

Jika ∆ → 0, maka gradient tali busur mendekati gradient garis singgung, sehingga
dapat dituliskan

78
