Page 299 - analysinew

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
299

7. ΘΕΩΡΗΜΑ BOLZANO (ΑΝΟΙΚΤΑ ΑΚΡΑ ± )
Έστω η συνάρτηση f: συνεχής στο 0 με f(0)=0, για
την οποία ισχύει
1
4
xf(x)+x συν x = 0, για καθε χ *
α) Να βρεθούν τα όρια: lim f(x) και lim f(x)
x - x +
β) Να αποδείξετε ότι η εξίσωση f(χ)=0 έχει μία τουλάχι-
στον πραγματική λύση.

α )
Για χ 0 η δοσμένη σχέση
γ ρ άφεται ισοδύναμα
1
xf(x)+x συν = 0`
4
x
f(x)=-x συν 1 , χ * (1)
3
x
Είναι

(1 )
lim f(x)= lim -x συν 1
3
x - x - x
1
=- lim x συν
3
x - x

=-(- ) 1
(1 )
lim f(x)= lim -x συν 1 =- lim x συν 1 =-(+ ) 1
3
3
x + x + x x + x

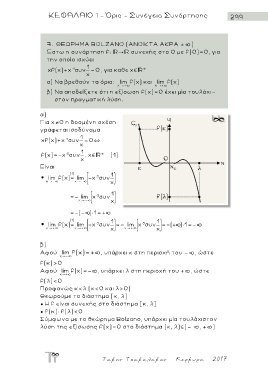
β )
Αφού lim f(x)= + , υπάρχει κ στη περιοχή του - , ώστε
x -
f(κ)>0
Αφού lim f(x)=- , υπάρχει λ στη περιοχή του + , ώστε
x +
f(λ)<0
Προφανώς κ<λ (κ<0 και λ>0)
Θεωρούμε το διάστημα [κ, λ]

● Η f είναι συνεχής στο διάστημα [κ, λ]
● f(κ) f(λ)<0
Σύμφωνα με το θεώρημα Bolzano, υπάρχει μία τουλάχιστον

λύση της εξίσωσης f(x)=0 στο διάστημα (κ, λ) (- , + )

Τακης Τσακαλακος Κερκυρα 2017