Page 305 - analysinew

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
305

5. ΘΕΩΡΗΜΑ BOLZANO (ΜΟΝΑΔΙΚΟ ξ ...)
Αν η συνάρτηση f είναι συνεχής και γνησίως αύξουσα στο
διάστημα [1, e] με 0 < f(x) < 1 για κάθε x [1, e]
Να αποδείξετε ότι υπάρχει μόνο ένα ξ (1, e) ώστε:
f(ξ) + ξ ∙ lnξ = ξ .

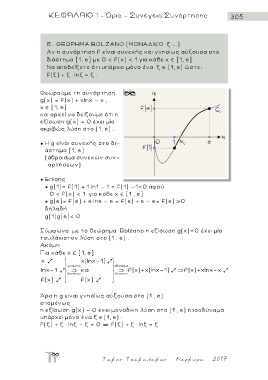
Θεωρούμε τη συνάρτηση
g(x) = f(x) + xlnx - x ,
x [1, e]
και αρκεί να δείξουμε ότι η
ε ξ ίσωση g(x) = 0 έχει μία
ακριβώς λύση στο (1, e) .

● Η g είναι συνεχής στο δ ι -
άστημα [1, e]
(άθροισμα συνεχών συν-
αρτήσεων)

● Επίσης
● g(1)= f(1) + 1 ln1 - 1 = f(1) -1<0 αφού
0 < f(x) < 1 για κάθε x [1 , e]
● g(e)= f(e) + e lne - e = f(e) + e - e= f(e) >0
δηλαδή
g(1)g(e)< 0

Σύμφωνα με το θεώρημα Bolzano η εξiσωση g(x)=0 έχει μία
τουλάχιστον λύσ η στο (1 , e) .
Ακόμη
Για κάθε x [1, e]
x x(lnx-1)

lnx-1 και f(χ) x(lnx-1) ~f(χ) xlnx-χ
f(χ) f(χ)

Άρα η g είναι γνησίως αύξουσα στο (1 , e)
επομένως
η εξίσωση g(x) = 0 έχει μοναδικη λύση στο (1 , e) η ισοδύναμα
υπάρχει μόνο ένα ξ ∈ (1, e) :
f(ξ) + ξ ∙ lnξ - ξ = 0 ~ f(ξ) + ξ ∙ lnξ = ξ

Τακης Τσακαλακος Κερκυρα 2017