Page 309 - analysinew

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
309

3. ΘΕΩΡΗΜΑ BOLZANO (ΔΥΟ ΛΥΣΕΙΣ ΑΚΡΙΒΩΣ)
α) Να αποδείξετε ότι η εξίσωση χ +2χ -1 =0 έχει δύο μόνο
4
2
λύσεις στο .
β) Να αποδείξετε οτι η εξίσωση
α ( x -μ)(x - ν) + β(x - λ)(x - ν) + γ((x - λ)(x - μ) = 0 ,
όπου α, β, γ > 0 και λ < μ < ν, έχει δύο ρίζες άνισες ,

μία στο διάστημα (λ, μ) και μία στο (μ, ν).

α )
Moνοτονία

f(x )-f(x )
λ= 1 2
x -x 2
1
=(x +x )(x +x +2)
2
2
1 2 1 2
Έτσι
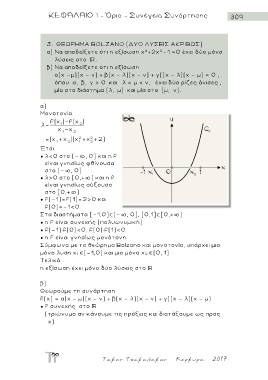
● λ<0 στο (- , 0] και η f
είναι γνησίως φθίνουσα
στο (- , 0]
● λ>0 στο [0,+ ) και η f
είναι γνησίως αύξουσα
στο [0,+ )
● f(-1)=f(1)=2>0 και
f(0)=-1<0
Στα διαστήματα [-1,0] (- , 0], [0,1] [0,+ )
● η f είναι συνεχής (πολυωνυμική)

● f(-1) f(0)<0, f(0) f(1)<0
● η f είναι γνησίως μονότονη
Σύμφωνα με το θεώρημα Bolzano και μον ο τονία, υπάρχει μια

μόνο λυση χ 1 (-1,0) και μια μόνο χ 2 (0, 1)
Τελικά
η ε ξ ίσωση έχει μόνο δύο λύσεις στο

β )
Θεωρούμε τη συνάρτηση
f(x) = α(x – μ)(x – ν) + β(x – λ)(x – ν) + γ((x – λ)(x – μ )
● f συνεχής στο
(τριώνυμο αν κάνουμε τις πράξεις και διατάξουμε ως προς
x)

Τακης Τσακαλακος Κερκυρα 2017