Page 308 - analysinew

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
308

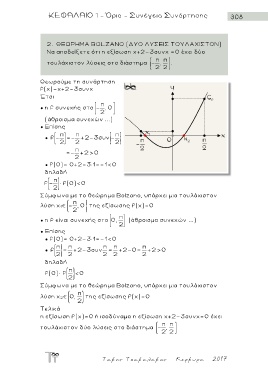
2. ΘΕΩΡΗΜΑ BOLZANO (ΔΥΟ ΛΥΣΕΙΣ ΤΟΥΛΑΧΙΣΤΟΝ)
Να αποδείξετε ότι η εξίσωση χ+2-3συνχ =0 έχει δύο
π π
, .
τουλάχιστον λύσεις στο διάστημα 2 2

Θεωρούμε τη συνάρτηση
f(x)=χ+2-3συνχ
Έτσι
π
● η f συνεχής στο , 0
2
(άθροισμα συνεχών ...)
● Επίσης
π π π
● f =- +2-3συν -
2 2 2

=- π +2 0
2

● f(0)= 0+2-3 1=-1<0
δηλαδή
π
f f(0)<0
2
Σύμφωνα με το θεώρημα Bolzano, υπάρχει μια τουλάχιστον
π
λύση χ 1 , 0 της εξίσωσης f(χ)=0
2
π
● η f είναι συνεχής στο 0, (άθροισμα συνεχών ...)
2
● Επίσης
● f(0)= 0+2-3 1=-1<0

● f π = π +2-3συν π π +2-0= π +2 0
2 2 2 2 2

δηλαδή
π
f(0) f <0
2
Σύμφωνα με το θεώρημα Bolzano, υπάρχει μια τουλάχιστον
π
λύση χ 2 0, της εξίσωσης f(χ)=0
2
Τελικά

η εξίσωση f(χ)=0 ή ισοδύναμα η εξίσωση χ+2-3συνχ=0 έχει
π π
τουλάχιστον δύο λύσεις στο διάστημα ,
2 2

Τακης Τσακαλακος Κερκυρα 2017