Page 313 - analysinew

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
313

ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ

Aν μία συνάρτηση f:
● είναι σ υ ν ε χ ή ς στο κλειστό διάστημα [α, β]
● ισχύει f ( α ) f ( β )

τότε για κάθε αριθμό n που βρίσκεται μ ε τ α ξ ύ των f(α),
f(β) υπάρχει ένα τουλάχιστον x 0 (α, β), τέτοιο ώστε να
ισχύει: f ( x 0 ) = n.

AΠΟΔΕΙΞΗ

Υποθέτουμε ότι f(α)<f(β)
Τότε θα ισχύει f(α)<η<f(β)

Θεωρούμε τη συνάρτηση

g(x)=f(χ)-η, χ [α, β]
Έτσι

● η g συνεχής στο[α, β]

● g(α) g(β)<0, αφου
● g(α) = f(α)-η <0

● g(β) = f(β)-η >0

Σύμφωνα με το θεώρημα
Bolzano, υπάρχει χ 0 (α, β)

τ έ τοιο, ώστε

g(χ 0)=0`f(χ 0)-η=0`
f(χ 0)=η

Ερμηνεία (Γεωμετρία )

Γεωμετρικά το θεώρημα
ενδιάμεσων τιμών ερμη-

νεύεται ως εξής :

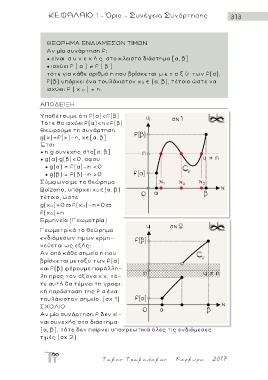
Aν από κάθε σημείο n που
β ρ ίσκεται μεταξύ των f(α)

και f(β) φέρουμε παράλλη-

λη προς τον άξονα x’x, τ ό -
τ ε αυτή θα τέμνει τη γραφι-

κή παράσταση της f σ’ένα

τουλάχιστον σημείο. (σχ 1)
ΣΧΟΛΙΟ

Αν μία συνάρτηση f δεν εί-

ναι συνεχής στο διάστημα
[α, β], τότε δεν παίρνει υποχρεωτικά όλες τις ενδιάμεσες

τιμές (σχ 2)

Τακης Τσακαλακος Κερκυρα 2017