Page 314 - analysinew
P. 314
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
314
ΠΑΡΑΤΗΡΗΣΕΙΣ
● Εναλλακτικά, το συμπέρασμα του θ ε ωρήματος ενδιάμεσων
τιμών μπορεί να είναι:
" ... υπάρχει τουλάχιστον μία ρίζα της εξίσωσης f(x) = n στο
διάστημα (α, β)"
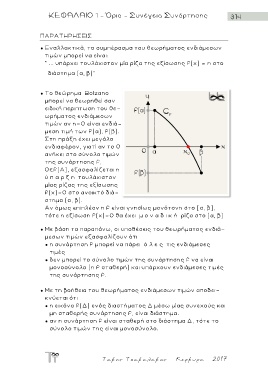
● Το θεώρημα Βolzano
μπορεί να θεωρηθεί σαν
ειδική περιπτωση του θ ε -
ωρήματος ενδιάμεσων
τιμών αν η=0 είναι ενδιά-
μεση τιμή των f(α), f(β).
Στη πράξη έχει μεγάλο
ενδιαφέρον, γιατί αν το 0
ανήκει στο σύνολο τιμών
της συνάρτησης f,
0 f(Α), εξασφαλίζ ε τ αι η
ύ π α ρ ξ η τουλάχιστον
μίας ρίζα ς της ε ξ ίσωσης
f(χ)=0 στο ανοικτό διά-
στημα (α, β).
Αν όμως επιπλέον η f είναι γνησίως μονότονη στο [α, β],
τότε η εξίσωση f(χ)=0 θα έχει μ ο ν α δ ι κ ή ρίζα στο (α, β)
● Με βάση τα παραπάνω, οι υποθέσεις του θ ε ωρήματος ενδιά-
μεσων τιμών εξασφαλίζουν ότι
● η συνάρτηση f μπορεί να πάρει ό λ ε ς τις ενδιάμεσες
τιμές
● δεν μπορεί το σύνολο τιμών της συνάρτησης f να είναι
μον ο σύνολο (η f σταθερή) και υπάρχουν ενδιάμεσες τιμές
της συνάρτησης f.
● Με τη βοήθεια του θ ε ωρήματος ενδιάμεσων τιμών α π οδει-
κνύεται ότι
● η εικόνα f(Δ) ενός διασ τ ήματος Δ μέσω μίας συνεχούς και
μη σταθερής συνάρτησης f, είναι διάστημα.
● αν η συνάρτηση f είναι σταθερή στο διάστημα Δ, τότε το
σύνολο τιμών της είναι μον ο σύνολο.
Τακης Τσακαλακος Κερκυρα 2017