Page 319 - analysinew

ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
319

ΠΑΡΑΔΕΙΓΜΑΤΑ

1. ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ (ΤΙΜΕΣ)
Δίνεται η συνάρτηση f με τύπο:
f(χ)=5ημ 2χ-3συν3χ+ημχ,
2
π
είναι ορισμένη στο διάστημα 0, 2 .

Να εξετάσετε αν οι τιμές -2, -1 και 0, είναι τιμές της συν-
άρτησης f.

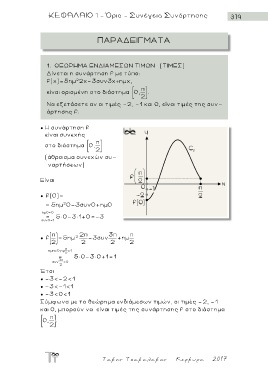
● Η συνάρτηση f
είναι συνεχής
π
στο διάστημα 0,
2
(άθροισμα συνεχών συ-

ναρτήσεων)

Είναι

● f(0)=

2
= 5ημ 0-3συν0+ημ0
ημ0 = 0
= 5× 0-3× 1+0=- 3
συν0 = 1

π 2π 3π π
● f =5ημ 2 -3συν +ημ
2 2 2 2
π
ημπ = 0, ημ = 1
= 2 5× 0-3× 0+1=1
συν 3π = 0
2
Έτσι
● -3<-2<1
● -3<-1<1
● -3<0<1

Σύμφωνα με το θεώρημα ενδιάμεσων τιμών, οι τιμές -2, -1
και 0, μπορούν να είναι τιμές της συνάρτησης f στο διάστημα
π
0, .
2

Τακης Τσακαλακος Κερκυρα 2017