Page 320 - analysinew
P. 320
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης
320
2. ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ (ΤΙΜΕΣ)
Δίνεται η συνάρτηση f με τύπο: f(χ)= x 3x+1-x +3x+1
2
Να σποδείξετε ότι υπάρχουν χ 1, χ 2 [1, 8] ώστε
f (χ 1)+f (χ 2)-4f(χ 1)-6f(χ 2)+13=0
2
2
● Για χ 1, χ 2 [1, 8] η δοσμένη σχέση γίνεται διαδοχικά
f ( χ 1)+f (χ 2)-4f(χ 1)-6f(χ 2)+13=0`
2
2
2
f (x )-2× 2× f(x )+2 2 +f (x )-2× 3× f (x )+3 2 = 0
2
2
1
1
2
(f (x )-2) 2 = 0 f (x )= 2
(f (x )-2) 2 +(f (x )-3) 2 = 0 ` 1 ` 1
2
1
(f (x )-3) 2 = 0 f (x )= 3
2
2
Αρκεί να δείξουμε ότι υ-
πάρχουν χ 1, χ 2 [1, 8] τέ-
τοια, ώστε οι αριθμοί 2 και
3 να είναι τιμές της συν-
άρτησης
Έτσι
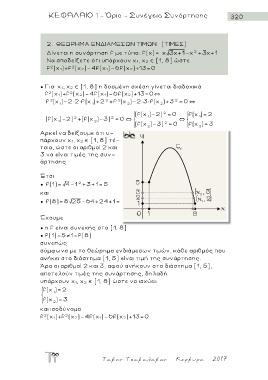
● f(1)= 4-1 2 +3+1= 5
και
● f(8)= 8 25-64+24+1= 1
Έχουμε
● η f είναι συνεχής στο [1, 8]
● f(1)=5 1=f(8)
συνεπώς
σύμφωνα με το θεώρημα ενδιάμεσων τιμών, κάθε αριθμός που
ανήκει στο διάστημα [1, 5] είναι τιμή της συνάρτησης.
Άρα οι αριθμοί 2 και 3, αφού α ν ήκουν στο διάστημα [1, 5],
α π οτελούν τιμές της συνάρτησης, δηλαδή
υπάρχουν χ 1, χ 2 [1, 8] ώστε να ισχύει:
f (x )= 2
1
f (x )= 3
2
και ισοδύναμα
f (χ 1)+f (χ 2)-4f(χ 1)-6f(χ 2)+13=0
2
2
Τακης Τσακαλακος Κερκυρα 2017