Page 306 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 306

Θ Ε Ω Ρ Ι Α ...

ΟΡΙΣΜΟΣ
Μία συνάρτηση f με πεδίο ορισμού Α, θα λέμε ότι παρουσιά-

ζει στο x 0 A
 Τ ο π ι κ ό Μ έ γ ι σ τ ο , αν υπάρχει δ > 0, τέτοιο ώστε:

για κάθε x A ( x 0 - δ, x 0 + δ), να ισχύει f ( x ) f ( x 0 ) .
 Τ ο π ι κ ό E λ ά χ ι σ τ ο , αν υπάρχει δ > 0, τέτοιο ώστε:
για καθε x A ( x 0 - δ, x 0 + δ), να ισχυει f ( x ) f ( x 0 ) .
ΑΠΟΨΗ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ
 Το x 0 λέγεται θέσ η ή σημείο τοπικού μέγιστου ή ε λ άχ ι -

στου, ενώ το f(x 0 ) λέγεται τοπικό μέγιστο η ε λ άχιστο
ΑΠΟΨΗ ΤΑΚΗ ΤΣΑΚΑΛΑΚΟΥ
 Το x 0 λέγεται θέσ η ή τετμημένη τοπικού μέγιστου ή ε-
λάχιστου, ενώ το f(x 0 ) λέγεται μέγιστη η ε λ άχιστη τιμή

της f και το σημείο (x 0 , f(x 0 )) λέγεται τοπικό μέγιστο ή
ε λ άχιστο της γραφικής παράστασης της f.

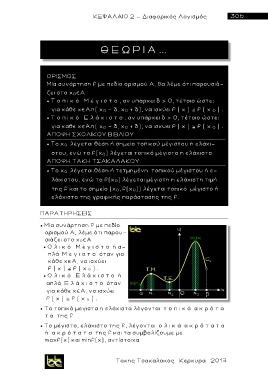
ΠΑΡΑΤΗΡΗΣΕΙΣ

 Μία συνάρτηση f με πεδίο

ορισμού Α , λέμε ότι παρου-

σ ι άζει στο x 0 A
 Ο λ ι κ ό Μ έ γ ι σ τ ο ή α-

π λ ά Μ ε γ ι σ τ ο όταν για

κάθε x A, να ισχύει
f ( x ) f ( x 0 ) .

 Ο λ ι κ ό E λ ά χ ι σ τ ο ή

απλά E λ ά χ ι σ τ ο όταν
για κάθε x A, να ισχύει
f ( x ) f ( x 0 ) .

 Τα τοπικά μεγιστα η ελάχιστα λέ γ ονται τ ο π ι κ ά α κ ρ ό τ α

τ α της f

 Το μέγιστο, ελάχιστο της f, λέγονται ο λ ι κ ά α κ ρ ό τ α τ α
ή α κ ρ ό τ α τ α της f και τα συμβολίζουμε με

maxf(x) και minf(x), αντίστοιχα

Τακης Τσακαλακος Κερκυρα 2017