Page 308 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 308

f(x)-f(x )
f'(x )= lim 0 0. (3)
0 x x + 0 x-x 0

Έτσι, από τις (2) και (3) έχουμε f’(x 0) = 0.

Ανάλογη η απόδειξη για τοπικό ε λ άχιστο.

Ερμηνεία (Γεωμετρία )
 f’ ( x 0)=0 σημαίνει ότι η εφαπτομένη της γραφικής παράστα-
σης στο σημείο(x 0,f(x 0)) είναι παράλληλη στον αξονα x’x
(σχήμα).

ΠΑΡΑΤΗΡΗΣΕΙΣ

 Το αντιστροφο του θεωρήματος Fermat δεν ισχύει παντα,
δηλαδή
ισχύει f’ ( x 0) = 0 ή

στο σημείο με τετμημένη το x 0 Δ η C f δέχεται οριζόντια
εφαπτομέν η
αλλά,

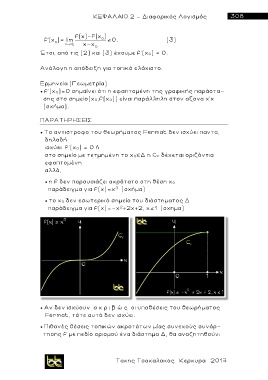
 η f δεν παρουσιάζει ακρότατο στη θέση x 0
παράδειγμα για f(x)=x (σχήμα)
3
 το x 0 δεν εσωτερικό σ η μ ε ίο του διάστηματος Δ

παράδειγμα για f(x)=-x +2x+2, x 1 (σχημα)
2

 Aν δεν ισχύουν α κ ρ ι β ώ ς οι υποθέσεις του θεωρήματος
Fermat, τότε αυτό δεν ισχύει.

 Πιθανές θέσεις τοπικών ακροτάτων μίας συνεχούς συνάρ-

τησης f με πεδίο ορισμού ένα διάστημα Δ, θα αναζητηθούν:

Τακης Τσακαλακος Κερκυρα 2017