Page 310 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 310

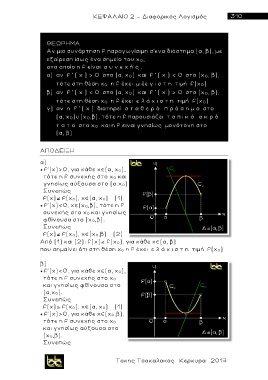
ΘΕΩΡΗΜΑ
Αν μια συνάρτηση f παραγωγίσιμη σ'ενα διάστημα (α, β), με
εξαίρεση ίσως ένα σημείο του x 0 ,
στο οποίο η f είναι σ υ ν ε χ ή ς .
α) αν f ’ ( x ) > 0 στο (α, x 0 ) και f ’ ( x ) < 0 στ ο (x 0 , β),

τότε στη θέση x 0 η f έχει μ έε γ ι σ τ η τιμή f(x 0 )
β) αν f ’ ( x ) < 0 στο (α, x 0 ) και f ’ ( x ) > 0 στ ο (x 0 , β),
τότε στη θέση x 0 η f έχει ε λ ά χ ι σ τ η τιμή f(x 0 )
γ) αν η f ’ ( x ) διατηρεί σ τ α θ ε ρ ό π ρ ό σ η μ ο στο
(α, x 0 )∪(x 0 ,β), τότε η f παρουσιάζει τ ο π ι κ ό α κ ρ ό
τ α τ ο στο x 0 και η f ειναι γνησίως μονότονη στο

(α, β)

ΑΠΟΔΕΙΞΗ
α )
 f'(x)>0, για κάθε x (α, x 0),

τότε η f συνεχής στο x 0 και

γνησίως αύξουσα στο (α,x 0)
Συνεπώς

f(x) f(x 0), x (α, x 0) (1)

 f'(x)<0, x (x 0,β), τότε η f
συνεχής στο x 0 και γνησίως

φθίνουσα στο (x 0,β).

Συνεπώς
f(x) f(x 0), x (x 0,β) (2)

Από (1) και (2): f(x) f(x 0), για κάθε x (α, β)

που σημαίνει ότι στη θέση x 0 η f έχει ε λ ά χ ι σ τ η τιμή f(x 0)

β)

 f'(x)<0, για κάθε x (α, x 0),
τότε η f συνεχής στο x 0

και γνησίως φθίνουσα στο

(α,x 0).
Συνεπώς

f(x) f(x 0), x (α, x 0) (1)

 f'(x)>0, για κάθε x (x 0,β),
τότε η f συνεχής στο x 0

και γνησίως αύξουσα στο

(x 0,β).
Συνεπώς

Τακης Τσακαλακος Κερκυρα 2017