Page 315 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 315

3. EΥΡΕΣΗ ΠΑΡΑΜΕΤΡΩΝ
Δίνεται η συνάρτηση f: , με τύπο
f(x)=χ -3αχ +3βχ+2α-β-3
2
3
η οποία, στη θέση χ=1 παρουσιάζει τοπικό μέγιστο με
τεταγμένη 2.
Να βρεθούν οι τιμές των α και β.

● Πεδίο ορισμού : Α=
● Για κάθε χ
● η f είναι συνεχής
(πολυωνυμική)
● η f είναι παραγωγίσιμη
(πολυωνυμική) με

f'(x)=(χ -3αχ +3βχ+
3
2
+2α-β-3)'
= 3χ -6αχ+3β
2
● Για χ=1, ικανοποι ο ύνται οι
υποθέσεις του θεωρήμα-
τος Fermat και

f(1) 2 1-3α+3β+2α-β-3 2
~
f'(1) 0 3-6α+3β 0

-α+2β 4 -2α+4β 8 ( ) 3β 9 β 3
~ ~ ~ ~
2α-β 1 2α-β 1 2α-β 1 2α-3 1

β 3 α= 2
~ ~
2α 4 β= 3
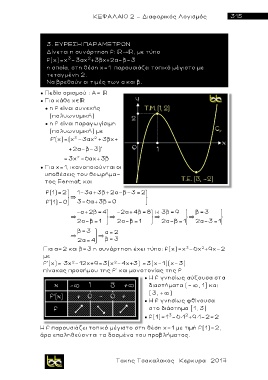
Για α=2 και β=3 η συνάρτηση έχει τύπο: f(x)=χ -6χ +9χ-2
3
2
με
f'(x)= 3χ -12χ+9=3(χ -4χ+3) =3(χ-1 ) ( χ -3)
2
2
πίνακας προσήμου της f' και μονοτονίας της f
● H f γνησίως αύξουσα στa
διαστήματα (- , 1] και
[3, + )
● H f γνησίως φθίνουσα

σ τ o διάστημα [1, 3)
2
3
● f(1)=1 -6 1 +9 1-2=2

Η f παρουσιάζει τοπικό μέγιστο στη θέση χ=1 με τιμή f(1)=2,
άρα επαληθεύονται τα δοσμένα του προβλήματος.

Τακης Τσακαλακος Κερκυρα 2017