Page 316 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 316

4. EΥΡΕΣΗ ΣΧΕΣΗΣ ΠΑΡΑΜΕΤΡΩΝ
Δίνεται η συνάρτηση f: , με τύπο
f(x)=χ +αχ +βχ+γ
2
3
η οποία παρουσιάζει δύο τοπικά ακρότατα.
2
Να αποδείξετε ότι α >3β.

● Πεδίο ορισμού :
Α=
● Για κάθε χ
● η f είναι συνεχής
(πολυωνυμική)
● η f είναι παραγωγίσιμη
(πολυωνυμική) με

3
2
f'(x)=(χ +αχ +βχ+γ)'

=3χ +2αχ+β
2
● Αφού η f παρουσιάζει
δύο τοπικά ακρότατα, η
εξίσωση f'(x)=0 πρέπει
να έχει δύο πράγματικες
και άνισες λύσεις,
δηλαδή πρέπει να ισχύει
Δ>0 `(2 α ) 2 -4 3 β>0
`4α -12β>0
2
`4(α -3β)>0
2
`α -3β>0
2
`α > 3 β
2

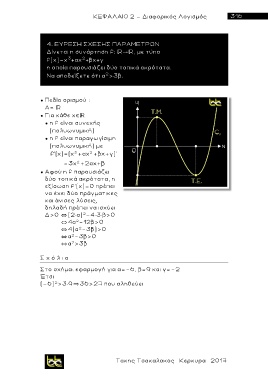
Σ χ ό λ ι ο

Στο σχήμα: εφαρμογή για α=-6, β=9 και γ=-2
Έτσι
2
(-6) >3 9~36>27 που αληθεύε ι

Τακης Τσακαλακος Κερκυρα 2017