Page 317 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 317

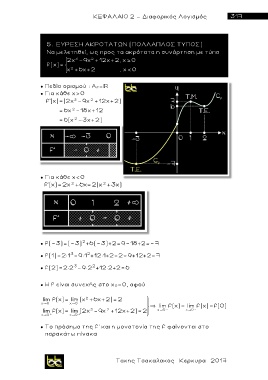
5. ΕΥΡΕΣΗ ΑΚΡΟΤΑΤΩΝ (ΠΟΛΛΑΠΛΟΣ ΤΥΠΟΣ)
Να μελετηθεί, ως προς τα ακρότατα η συνάρτηση με τύπο
2x -9x +12x+2, x 0
3
2
f(x)=
2
x +6x+2 , x 0

● Πεδίο ορισμού : Α f=
● Για κάθε χ>0
f'(x)=(2x -9x 2 +12x+2)'
3
2
= 6x -18x+12

2
= 6(x -3x+2)
= 6(x-1)(x-2)

● Για κάθε χ<0
2
2
f'(x)=2x +6x =2(x +3x)

2
● f(-3)=(-3) +6(-3)+2=9-18+2=-7

3
2
● f(1)=2 1 -9 1 +12 1+2=2-9+12+2=7
3
2
● f(2)=2 2 -9 2 +12 2+2=6

● H f είναι συνεχής στο χ 0=0, αφού

lim f(x)= lim (x + 6x+2)= 2
2
x 0 x 0 ~ lim f(x) lim f(x) f(0)
3
lim f(x)= lim (2x -9x 2 +12x+2)= 2 x 0 x 0
x 0 x 0

● Το πρόσημο της f' και η μονοτονία της f φ α ίνονται στο
παρακάτω πίνακα

Τακης Τσακαλακος Κερκυρα 2017