Page 311 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 311

f(x) f(x 0), για κάθε x (x 0,β) (2)
Από (1) και (2):
f(x) f(x 0), για κάθε x (α, β)
που σημαίνει ότι στη θέση x 0 η f έχει μ έ γ ι σ τ η τιμή f(x 0)

γ )

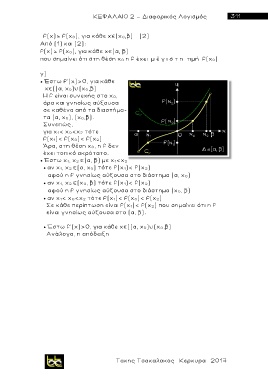
 Έστω f'(x)>0, για κάθε
x ((α, x 0)∪(x 0,β)
Η f είναι συνεχής στο x 0,
άρα και γνησίως αύξουσα
σε καθένα α π ό τ α διασ τ ήμα-
τα (α, x 0), (x 0,β).
Συνεπώς,
για x 1< x 0<x 2 τότε
f(x 1)< f(x 0)< f(x 2)
Άρα, στη θέση x 0, η f δεν
έχει τοπικό ακρότατο.

 Έστω x 1, x 2 (α, β) με x 1<x 2
 αν x 1, x 2 (α, x 0) τότε f(x 1)< f(x 2)
αφού η f γνησίως αύξουσα στο διάστημα (α, x 0)
 αν x 1, x 2 (x 0, β) τότε f(x 1)< f(x 2)
αφού η f γνησίως αύξουσα στο διάστημα (x 0, β)
 αν x 1< x 0<x 2 τότε f(x 1)< f(x 0)< f(x 2)
Σε κάθε περίπτωση είναι f(x 1)< f(x 2) που σημαίνει ότι η f
είναι γνησίως αύξουσα στο (α, β).

 Έστω f'(x)>0, για κάθε x ((α, x 0) ∪ ( x 0,β)
Ανάλογα, η απόδειξη

Τακης Τσακαλακος Κερκυρα 2017