Page 307 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 307

 Το μέγιστο (ελάχιστο) της συνάρτησης f, είναι μεγαλύτερο
(μικρότερο) από τα τοπικά μέγιστα (ελάχιστα) της f.

 Το τοπικό μέγιστο της συνάρτησης f, μπορεί να είναι μικρό-
τερο από ένα τοπικό ελάχιστο και αντίστροφα.
 Τ ο ολικό ακρότατο της συνάρτησης f είναι και τοπικό ακρό-
τατο της.
Δεν ισχύει το αντίστροφο.

ΘΕΩΡΗΜΑ FERMAT

Αν μία συνάρτηση f είναι :
 Ο ρ ι σ μ έ ν η σ'ένα διάστημα Δ
 Π α ρ α γ ω γ ί σ ι μ η σε εσωτερικό σημείο ξ του Δ
 Παρουσιάζει τ ο π ι κ ό α κ ρ ό τ α τ ο στο ξ
τότε ισχύει: f ' ( ξ ) = 0 .

AΠΟΔΕΙΞΗ

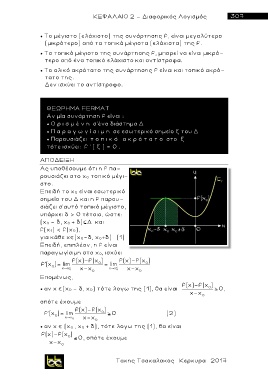
Ας υποθέσουμε ότι η f πα-

ρουσιάζει στο x 0 τοπικό μέγ ι -
στο.

Επειδή το x 0 είναι εσωτερικό

σημείο του Δ και η f παρου-
σιάζει σ’αυτό τ ο πικό μέγιστο,

υπάρχει δ > 0 τέτοιο, ώστε:

(x 0 - δ, x 0 + δ) Δ και
f(x 1) < f(x 0),

για κάθε x (x 0-δ, x 0+δ) (1)

Επειδή, επιπλέον, η f είναι

παραγωγίσιμη στο x 0, ισχύει

f'(x )= lim f(x)-f(x ) = lim f(x)-f(x )
0
0
0 x x - 0 x-x x x + 0 x-x
0 0
Επομένως,
f(x)-f(x )
 αν x (x 0 - δ, x 0) τότε λογω της (1), θα είναι 0 0,
x-x 0
οπότε έχουμε

f'(x )= lim - 0 f(x)-f(x ) 0 (2)
0

0
x-x
x x
0
 αν x (x 0 , x 0 + δ), τότε λογω της (1), θα είναι

f(x)-f(x )
0 0, οπότε έχουμε
x-x 0

Τακης Τσακαλακος Κερκυρα 2017