Page 342 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 342

Θ Ε Ω Ρ Ι Α ...

ΟΡΙΣΜΟΣ
Αν μια συνάρτηση f είναι σ υ ν ε χ ή ς σ'ενα διάστημα Δ και
π α ρ α γ ω γ ί σ ι μ η (τουλάχιστον) στα ε σ ω τ ε ρ ι κ ά σ η
μ ε ί α του Δ, θα λέμε:
 H f στρέφει τ α κ ο ί λ α π ρ ο ς τ α π ά ν ω , η είναι
κ υ ρ τ ή στο Δ, αν
η f’ είναι γνήσια αύξουσα στο ε σ ω τ ε ρ ι κ ό του Δ.
 H f στρέφει τ α κ ο ί λ α π ρ ο ς τ α κ ά τ ω , η είναι
κ ο ί λ η στο Δ, αν
η f’ είναι γνήσια φθίνουσα στο ε σ ω τ ε ρ ι κ ό του Δ.

ΠΑΡΑΤΗΡΗΣΕΙΣ

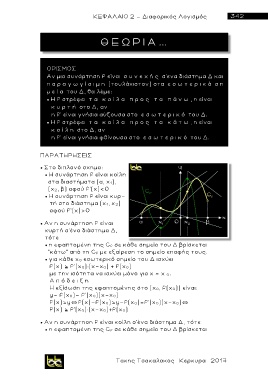
 Στο διπλανό σχημα:
 Η συνάρτηση f είναι κ ο ίλ η

στα διαστήματα (α, χ 1),

(χ 2, β) αφού f'(x)<0
 Η συνάρτηση f είναι κ υ ρ -

τή στο διάστημα (χ 1, χ 2)

αφού f'(x)>0

 Αν η συνάρτηση f είναι
κυρτή σ'ένα διάστημα Δ,

τότε

 η εφαπτομένη της C f σε κάθε σημείο του Δ βρίσκεται
"κάτω" από τη C f με εξαίρεση το σημείο επαφής τους.

 για κάθε x 0 εσωτερικό σημείο του Δ ισχύει

f(x) f'(x 0) ( χ -x 0) + f(x 0)
με την ισότητα να ισχύει μόνο για χ = x 0.

Α π ό δ ε ι ξ η

Η εξίσωση της εφαπτομένης στο (x 0, f(x 0)) είναι:
y- f(x 0)= f'(x 0) ( χ -x 0)

f(x) y`f(x)-f(x 0) y-f(x 0)=f'(x 0) ( χ -x 0)`

f(x) f'(x 0) (χ-x 0)+f(x 0)

 Αν η συνάρτηση f είναι κ ο ίλ η σ'ένα διάστημα Δ, τότε

 η εφαπτομένη της C f σε κάθε σημείο του Δ βρίσκεται

Τακης Τσακαλακος Κερκυρα 2017