Page 347 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 347

ΒΑΣΙΚΕΣ ΠΡΟΤΑΣΕΙΣ

1. (JENSEN)
Δίνεται η παραγωγίσιμη συνάρτηση f σ' ενα διάστημα [α, β].

Να αποδ ε ίξετε ότι
α) αν η f στρέφει τα κοίλα κάτω στο [α, β] τότε
f α+β > f(α)+f(β)
2 2
β) αν η f στρέφει τα κοίλα άνω στο [α, β] τότε

α+β f(α)+f(β)
f 2 < 2

ΑΠΟΔΕΙΞΗ

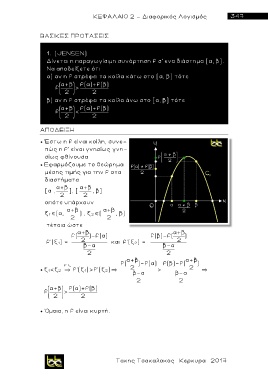
 Έστω η f είναι κ ο ίλη, συνε-

πώς η f' είναι γνησίως γνη-

σίως φθίνουσα
 Εφαρμόζουμε το θεώρημα

μέσης τιμής για την f στα

δ ι αστήματα

[α , α+β ], [ α+β , β]
2
2

οπότε υ π άρχουν
α+β α+β
ξ 1 (α, 2 ) , ξ 2 ( 2 , β)

τέτοια ώστε
α+β α+β
f( )-f(α) f(β)-f( )
f'(ξ 1) = 2 και f'(ξ 2) = β-α 2

β-α
2 2
α+β α+β
f' f( )-f(α) f(β)-f( )
 ξ 1<ξ 2 f'(ξ 1)>f'(ξ 2)~ 2 > 2 ~
β-α β-α
2 2
α+β f(α)+f(β)
f >
2 2

 Όμοια, η f είναι κυρτή.

Τακης Τσακαλακος Κερκυρα 2017