Page 352 - diaforikos
P. 352
ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 352
3. ΕΥΡΕΣΗ ΠΑΡΑΜΕΤΡΩΝ
Να βρεθούν οι τιμέ των α, β ώστε η συνάρτηση f με τύπο
f(x)=α χ 5 -(4β+2)χ +(α-1)χ+1
3
να έχει σημείο καμπής το Α(1, -4).
● Πεδίο ορισμού : Α=
● το Α(1, -4) είναι σημείο
της C f αρα
f(1)=- 4
3
5
α× 1 -(4β+2)× 1 +(α-1)× 1+
+1=- 4
α-4β-2+α-1+1 =- 4
2α-4β=- 2
α= 2β- 1 (1)
● Για κάθε χ
f είναι δύο φορές παρα-
γωγίσιμη (πολυωνυμική) με
● f'(x)=5αx -3(4β+2)x +(α-1)
2
4
2
3
● f''(x)=(5αx -3(4β+2)x +(α-1) )' =20αx -6(4β+2)x
4
● για να έχει σημείο καμπής το Α(1, -4) η f πρέπει
f"(x )=0 f"(1)=0 20α-6(4β+2)=0 5α-6β-3=0
0
(2)
5(2β- 1)-6β-3=0 10 -5-6β-3=0 β= 2
Από (1): α=2×2- 1 α=3
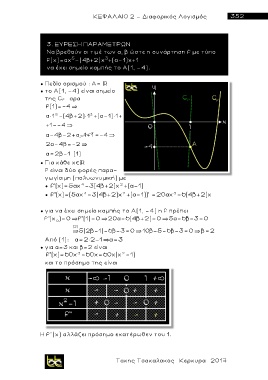
● για α=3 και β=2 είναι
f"(x)=60x -60x=60x(x -1)
2
3
και το πρόσημο της είναι
H f''(x) αλλάζει πρόσημο εκατέρωθεν του 1.
Τακης Τσακαλακος Κερκυρα 2017