Page 357 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 357

ΠΑΡΑΔΕΙΓΜΑΤΑ

1. ΑΠΟΔΕΙΞΗ ΑΝΙΣΟΤΗΤΑΣ - ΕΦΑΠΤΟΜΕΝΗ
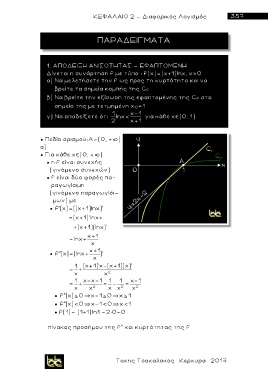
Δίνεται η συνάρτηση f με τύπο : f(x)=(x+1)lnx, x>0
α) Να μελετήσετε την f ως προς τη κυρτότητα και να
βρείτε τα σημεία καμπής της C f

β) Να βρείτε την εξίσωση της εφαπτομένης της C f στο
σημείο της με τετμημένη χ 0 =1

γ) Να αποδείξετε ότι 1 lnx< x-1 για κάθε χ (0, 1)
2 x+1

● Πεδίο ορισμού: Α = (0, + )
α )
● Για κάθε χ (0, + )
● η f είναι συνεχής
(γινόμενο συνεχών)
● f είναι δύο φορές πα-
ραγωγίσιμη
(γινόμενο παραγωγίσι-
μων) με

● f'(x)=((χ+1)lnχ)'
=(χ+1)' ln χ+

+(χ+1)(lnχ)'
χ+1
=ln χ+
χ
χ+1
● f''(x)=(lnχ+ )'
χ

1 (x+1)'x-(x+1)(x)'
= +
χ χ 2

= 1 + x-x-1 = 1 - 1 = -1
χ χ 2 χ χ 2 χ 2
● f''(x) 0~ χ-1 0~ χ 1
● f''(x)< 0~ χ-1 0~χ 1
● f(1)= (1+1)ln1 =2 0=0

πίνακας προσήμου της f'' και κυρτότητας της f

Τακης Τσακαλακος Κερκυρα 2017