Page 359 - diaforikos
P. 359
ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 359
2. ΑΠΟΔΕΙΞΗ ΑΝΙΣΟΤΗΤΑΣ - JENSEN
Δίνεται η συνάρτηση f: με τύπο :
f(x)=e
x
Να αποδείξετε ότι 2 e 2 <e +e για κάθε a,β
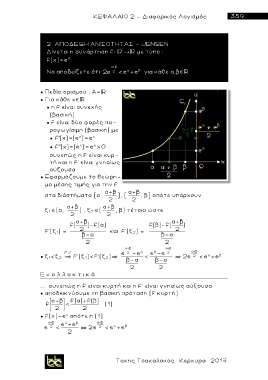
● Πεδίο ορισμού : Α=
● Για κάθε χ
● η f είναι συνεχής
(βασική)
● f είναι δύο φορές πα-
ραγωγίσιμη (βασική) με
● f'(x)=(e )' =e
x
x
x
x
● f''(x)=(e )' =e >0
συνεπώς η f είναι κυρ-
τή και η f' είναι γνησίως
αύξουσα
● Εφαρμόζουμε το θεώρη-
μα μέσης τιμής για την f
α+β α+β
στα διάστήματα [α , ], [ , β] οπότε υ π άρχουν
2 2
α+β α+β
ξ 1 (α, ) , ξ 2 ( , β) τέτοια ώστε
2 2
α+β α+β
f( )-f(α) f(β)-f( )
f'(ξ 1) = 2 και f'(ξ 2) = 2
β-α β-α
2 2
α+β α+β
β
f' e 2 -e α e -e 2 α+β
β
● ξ 1< ξ 2 f'(ξ 1)<f'(ξ 2)~ < ~ 2e 2 <e +e
α
β-α β-α
2 2
Ε ν α λ λ α κ τ ι κ ά
... συνεπώς η f είναι κυρτή και η f' είναι γνησίως αύξουσα
● α π οδεικνύουμε τη βασική π ρ όταση (f κυρτή)
α+β f(α)+f(β)
f < (1)
2 2
● f(x)=e οπότε η (1)
x
α+β e +e α+β
e 2 < ` 2e 2 < e +e
β
α
2
Τακης Τσακαλακος Κερκυρα 2017