Page 353 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 353

4. ΕΥΡΕΣΗ ΠΑΡΑΜΕΤΡΩΝ
Να αποδείξετε ότι για κάθε α *, η συνάρτηση f με τύπο :
f(x)=χ - 2αχ +6α χ -2α+1
4
3
2
2
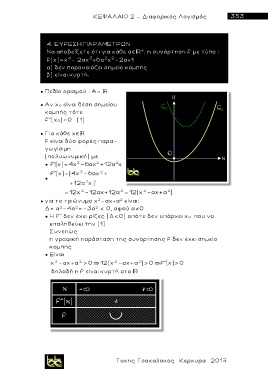
α) δεν παρουσιάζει σημείο καμπής
β) είναι κυρτή.

● Πεδίο ορισμού : Α=

● Αν χ 0 είναι θέση σημείου
καμπής τότε
f''(χ 0)=0 (1)

● Για κάθε χ
f είναι δύο φορές παρα-
γωγίσιμη
(πολυωνυμική) με
3
2
● f'(x)=4x -6αx +12α x
2
f''(x)=(4x -6αx 2 +
3
●
2
+12α x )'
2
=12x -12αx+12α =12(x -αx+α )
2
2
2
● για το τριώνυμο χ -αχ+α είναι:
2
2
Δ= α -4α =-3α < 0, αφού α 0
2
2
2
● Η f'' δεν έχει ρίζες (Δ<0) οπότε δεν υπάρχει χ 0 που να
επαληθεύει την (1)
Συνεπώς
η γραφική παράσταση της συνάρτησης f δεν έχει σημείο
καμπής
● Είναι
2
x -αx+α 2 > 0~ 12(x -αx+α )> 0~ f''(x)> 0
2
2
δηλαδή η f είναι κυρτή στο

Τακης Τσακαλακος Κερκυρα 2017