Page 403 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 403

2. ΕΠΙΛΟΓΗΣ
Έστω η συνάρτηση g συνεχής στο τέτοια, ώστε:
f(x)-e 2x +1
, x 0
g(x)= ημ2x
3 , x= 0

α) Aν f συνεχής στο , να υπολογίσετε το f(0).
β) Να αποδείξετε ότι η f είναι παραγωγίσιμη στο x = 0 .
γ) Έστω η συνάρτηση : h(x) = e –x ∙f(x) .
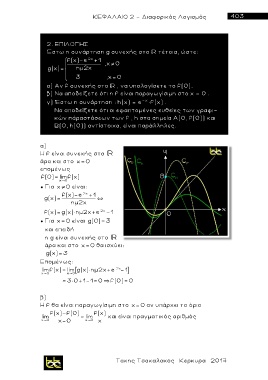
Να αποδείξετε ότι οι εφαπτομένες ευθείες των γραφι-
κών πάρασ τ άσεων των f , h στα σημεία Α(0, f(0)) και
Β(0, h(0)) αντίστοιχα, είναι παράλληλες.

α)

Η f είναι συνεχής στο
άρα και στο x=0
επομένως
f(0)= limf(x)
x 0
● Για x 0 είναι:
f(x)-e 2x +1
g(x)=
ημ2x

f(x)= g(x)× ημ2x+e 2x -1
● Για x=0 είναι g(0)=3
και επειδή

η g είναι συνεχής στο
άρα και στο x=0 θα ισχύει:
g(x)=3

Επομένως:
limf(x)= lim g(x)× ημ2x+e 2x -1
x 0 x 0
= 3× 0+1-1= 0 f(0)= 0

β)

Η f θα είναι παραγωγίσιμη στο x=0 αν υπάρχει το όριο
f(x)-f(0) f(x)
lim = lim και είναι πραγματικός αριθμός
x 0 x-0 x 0 x

Τακης Τσακαλακος Κερκυρα 2017