Page 407 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 407

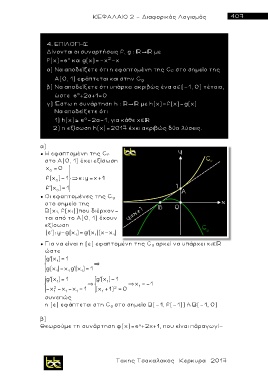
4. ΕΠΙΛΟΓΗΣ
Δίνονται οι συναρτήσεις f, g : με
f(x)=e και g(x)=-x -x
2
x

α) Nα αποδείξετε ότι η εφαπτομένη της C f στο σημείο της

Α(0, 1) εφάπτεται και στην C g
β) Nα αποδείξετε ότι υπάρχει ακριβώς ένα α (-1, 0) τέτοιο,
α
ώστε e +2α+1=0
γ) Έστω η συνάρτηση h : μ ε h(x)=f(x)-g(x)
Nα αποδείξετε ότι
1) h(x) e -2 α -1, για κάθε χ
α
2) η εξίσωση h(x)=2017 έχει ακριβώς δύο λύσεις.

α)
● Η εφαπτομένη της C f
στο Α(0, 1) έχει εξίσωση
x = 0
0
f(x )= 1 : y x 1
0
f'(x )= 1
0
● Οι εφαπτομένες της C g
στο σημείο της
Β(χ 1, f(x 1))που διέρχον-
ται από το Α(0, 1) έχουν
εξίσωση
(ε'): y-g(x )=g'(x )(x-x )
1
1
1

● Για να είναι η (ε) εφαπτομένη της C g αρκεί να υπάρχει χ 1
ώστε
g'(x )= 1
1
g(x )-x g'(x )= 1
1 1 1
g'(x )= 1 g'(x )= 1
1 1 x =- 1
2
2
- x -x -x = 1 (x +1) = 0 1
1
1
1
1
συνεπώς
η (ε) εφάπτεται στη C g στο σημείο Β ( -1, f(-1)) ή Β(-1, 0)

β )
Θεωρούμε τη συνάρτηση φ(χ)=e +2χ+1, που είναι πάραγωγί-
χ

Τακης Τσακαλακος Κερκυρα 2017