Page 410 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 410

5. ΕΠΙΛΟΓΗΣ
Δίνεται η συνάρτηση f(x)=xln(x+1)-(x+1)lnx, μ ε x>0
α) Nα αποδείξετε ότι:
1
1) ln(x+1)-lnx< , x>0
x
2) η f είναι γνησίως φθίνουσα στο διάστημα (0, + )
β) Nα υπολογίσετε το όριο
1
lim xln 1+
x + x
γ) Να αποδείξετε ότι υπάρχει μοναδικός αριθμός α (0,+ )
τέτοιος, ώστε (α + 1) α = α α + 1

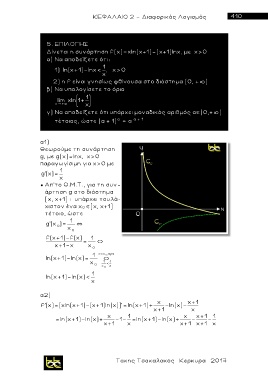
α1)
Θεωρούμε τη συνάρτηση
g, με g(x)=lnx, x>0
παραγωγίσιμη για χ>0 με

g'(x)= 1
x
● Απ'το Θ.Μ.Τ., για τη συν-
άρτηση g στο διάστημα
[χ, χ+1] : υπάρχει τουλά-

χιστον ένα χ 0 [χ, χ+1]
τέτοιο, ώστε
1
g'(x )= x
0
0

f(x+1)-f(x) = 1
x+1-x x
0 x < x αρα
ln(x+1)-ln(x)= 1 0
x 1 1
0 x 0 < x
1
ln(x+1)-ln(x)<
x

α2)
x x+1
f'(x)=[xln(x+1)-(x+1)ln(x)]' = ln(x+1) -ln(x)-
x+1 x
x 1 x x+1 1
= ln(x+1)-ln(x) -1- ln(x+1)-ln(x) - -
x+1 x x+1 x+1 x

Τακης Τσακαλακος Κερκυρα 2017