Page 117 - chapter 1

117
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

3. AΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ
Δίνεται η συνάρτηση f: με τύπο: f(x)=2χ +1
3
α) Να δείξετε οτι η συνάρτηση f είναι αντιστρέψιμη.
β) Να βρείτε τα κοινά σημεία των C και C - 1
f f
α )
Το πεδίο ορισμού της f εί-
ναι:Α=
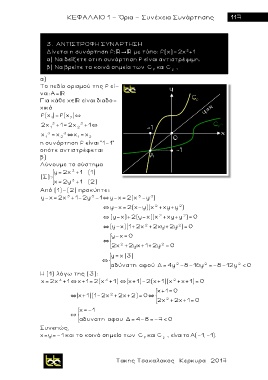
Για κάθε χ είναι διαδο-
χικά
f(x )= f(x )`
1 2
2x 1 3 +1= 2x 2 3 +1`
x 1 3 = x 2 3 `x = x 2
1
η συνάρτηση f είναι "1-1"
οπότε αντιστρέφεται
β )
Λύνουμε το σύστημα

y= 2x 3 +1 (1)
(Σ):
x= 2y 3 +1 (2)

Από (1)-(2) προκύπτει:
3
3
3
y-x= 2x 3 +1-2y -1 y-x= 2(x -y )
y-x= 2(x-y) (x 2 +xy+y )
2
(y-x)+2(y-x) (x 2 +xy+y )= 0
2
(y-x)(1+2x 2 +2xy+2y )= 0
2

y-x= 0

2
2x 2 +2yx+1+2y = 0
y= x (3)

αδύνατη αφού Δ= 4y - 8-16y =- 8-12y < 0
2
2
2
Η (1) λόγω της (3):
x= 2x 3 +1 x+1= 2(x 3 +1) (x+1)-2(x+1)(x 2 +x+1)= 0

x+1= 0
(x+1)(1-2x 2 +2x+2)= 0
2x 2 +2x+1= 0

x=- 1

αδυνατη αφου Δ= 4- 8=- 7< 0

Συνεπώς,
χ = y=-1 και το κοινό σημείο των C και C f - 1 είναι το A(-1, -1).
f

Τακης Τσακαλακος Κερκυρα 2017